Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 45, 46 sách giáo khoa Toán 11 tập 2 chương trình Kết nối tri thức. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án đầy đủ, kèm theo các bước giải chi tiết, giúp bạn dễ dàng theo dõi và áp dụng vào các bài tập tương tự.
Cho mặt phẳng (P) chứa đường thẳng b vuông góc với mặt phẳng (Q).
Video hướng dẫn giải
Cho mặt phẳng (P) chứa đường thẳng b vuông góc với mặt phẳng (Q). Lấy một đường thẳng a vuông góc với (P) (H.7.47).
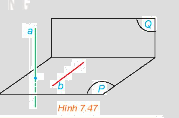
a) Tính góc giữa a và b.
b) Tính góc giữa (P) và (Q).
Phương pháp giải:
- Sử dụng 2 đường thẳng vuông góc thì góc giữa chúng bằng 900.
- Sử dụng nhận xét trang 45 để xác định góc giữa 2 mặt phẳng.
Lời giải chi tiết:
a) \(\left. \begin{array}{l}a \bot \left( P \right)\\b \subset \left( P \right)\end{array} \right\} \Rightarrow a \bot b \Rightarrow \left( {a,b} \right) = {90^0}\)
b) Gọi \(\left( P \right) \cap \left( Q \right) = \Delta \)
\(\begin{array}{l}a \bot \Delta \left( {a \bot \left( P \right)} \right)\\b \bot \Delta \left( {b \bot \left( Q \right)} \right)\\ \Rightarrow \left( {\left( P \right),\left( Q \right)} \right) = \left( {a,b} \right) = {90^0}\end{array}\)
Video hướng dẫn giải
Trong HĐ1 của Bài 23, ta đã nhận ra rằng đường thẳng nối các bản lề của cửa phòng vuông góc với sàn nhà. Hãy giải thích vì sao trong quá trình đóng – mở, cánh cửa luôn vuông góc với sàn nhà.
Phương pháp giải:
Hai mặt phẳng vuông góc với nhau nếu mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Lời giải chi tiết:
Trong một phòng, mặt sàn và các mặt tường đều vuông góc với nhau. Khi cánh cửa được đóng lại, thì mặt cửa cũng vuông góc với cả mặt sàn và mặt tường, nên đường thẳng nối bán lề của cánh cửa và cạnh của phòng sẽ là đường thẳng vuông góc với sàn nhà.
Trong quá trình đóng - mở cánh cửa, bán lề của cánh cửa vẫn cố định với mặt tường, nên đường thẳng nối bán lề của cánh cửa và cạnh của phòng vẫn là đường thẳng vuông góc với sàn nhà. Từ đó suy ra, trong quá trình đóng - mở, cánh cửa luôn vuông góc với sàn nhà.
Mục 2 trang 45, 46 SGK Toán 11 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Nội dung chính bao gồm các dạng bài tập về tính đơn điệu của hàm số lượng giác, tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác và giải phương trình lượng giác cơ bản. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Mục 2 bao gồm các bài tập từ 1 đến 6, mỗi bài tập tập trung vào một khía cạnh khác nhau của kiến thức đã học. Chúng ta sẽ đi vào giải chi tiết từng bài:
Bài 1 yêu cầu học sinh xét tính đơn điệu của các hàm số lượng giác trên một khoảng cho trước. Để giải bài này, cần nắm vững các kiến thức về đạo hàm của hàm số lượng giác và quy tắc xét dấu của đạo hàm. Ví dụ, nếu đạo hàm của hàm số dương trên một khoảng thì hàm số đồng biến trên khoảng đó, và ngược lại.
Bài 2 tập trung vào việc tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số lượng giác. Để giải bài này, có thể sử dụng phương pháp đạo hàm hoặc phương pháp lượng giác. Phương pháp đạo hàm đòi hỏi học sinh phải tính đạo hàm của hàm số và tìm các điểm cực trị. Phương pháp lượng giác dựa trên việc sử dụng các tính chất của hàm số lượng giác, chẳng hạn như biên độ và chu kỳ.
Các bài tập từ 3 đến 6 yêu cầu học sinh giải các phương trình lượng giác cơ bản. Để giải các phương trình này, cần nắm vững các công thức lượng giác cơ bản, chẳng hạn như công thức cộng và trừ góc, công thức nhân đôi và công thức hạ bậc. Ngoài ra, cần chú ý đến việc xác định đúng miền nghiệm của phương trình.
Ví dụ: Giải phương trình sin(x) = 1/2.
Giải: Phương trình sin(x) = 1/2 có nghiệm là:
Trong đó k là số nguyên.
Khi giải các bài tập về hàm số lượng giác, cần chú ý đến các vấn đề sau:
Hy vọng rằng với lời giải chi tiết và các phương pháp giải hiệu quả được trình bày trong bài viết này, các bạn học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 45, 46 SGK Toán 11 tập 2 - Kết nối tri thức. Chúc các bạn học tập tốt!