Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 3 trang 25, 26 sách giáo khoa Toán 11 tập 1 chương trình Kết nối tri thức. Bài viết này cung cấp đáp án đầy đủ, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Cho hàm số (y = sin x). a) Xét tính chẵn, lẻ của hàm số
Cho hàm số \(y = \sin x\).
a) Xét tính chẵn, lẻ của hàm số
b) Hoàn thành bảng giá trị sau của hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) bằng cách tính giá trị của \(\sin x\) với những x không âm, sau đó sử dụng kết quả câu a để suy ra giá trị tương ứng của \(\sin x\) với những x âm.
\(x\) | \( - \pi \) | \( - \frac{{3\pi }}{4}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{4}\) | 0 | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\pi \) |
\(\sin x\) | ? | ? | ? | ? | ? | ? | ? | ? | ? |
Bằng cách lấy nhiều điểm \(M\left( {x;\sin x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\).
c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kỳ \(T = 2\pi \), ta được đồ thị của hàm số \(y = \sin x\) như hình dưới đây.
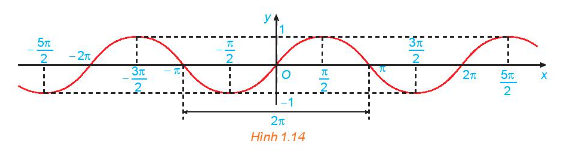
Từ đồ thị ở Hình 1.14, hãy cho biết tập giá trị, các khoảng đồng biến, các khoảng nghịch biến của hàm số \(y = \sin x\)
Phương pháp giải:
Sử dụng định nghĩa hàm số chẵn lẻ
Dựa vào đồ thị để xác định tập giá trị, các khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
a) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right) = - \sin x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \sin x\) là hàm số lẻ.
b)
\(x\) | \( - \pi \) | \( - \frac{{3\pi }}{4}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{4}\) | 0 | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\pi \) |
\(\sin x\) | \(0\) | \( - \frac{{\sqrt 2 }}{2}\) | \( - 1\) | \( - \frac{{\sqrt 2 }}{2}\) | 0 | \(\frac{{\sqrt 2 }}{2}\) | 1 | \(\frac{{\sqrt 2 }}{2}\) | 0 |
c) Từ đồ thị trên, ta thấy hàm số \(y = \sin x\) có tập xác định là \(\mathbb{R}\), tập giá trị là [-1;1] và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right),\;k\; \in \;\mathbb{Z}.\)
Tìm tập giá trị của hàm số \(y = 2\sin x\).
Phương pháp giải:
Tập giá trị của hàm số là tập min – max của hàm số trên tập xác định
Lời giải chi tiết:
Tập xác định của hàm số là \(D = \mathbb{R}\)
Vì
\( \Rightarrow \) Tập giá trị của hàm số \(y = 2\sin x\) là \(T = \left[ { - 2;2} \right]\).
Xét tình huống mở đầu.
a) Giải bài toán ở tình huống mở đầu
b) Biết rằng quá trình hít vào xảy ra khi v > 0 và quá trình thở ra khi v < 0. Trong khoảng thời gian từ 0 đến 5 giây, khoảng thời điểm nào thì người đó hít vào? Người đó thở ra?
Phương pháp giải:
Áp dụng công thức tính chu kỳ
Lời giải chi tiết:
a) Chu ký hô hấp: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{\pi }{3}}} = 6\left( s \right)\)
Số chu kỳ hô hấp trong 1 phút là \(\frac{60}{6}=10\)(chu kì).
b) Ta có: \(v=0,85\sin \frac{\pi t}{3}\)
+) v > 0 khi \(0,85\sin \frac{\pi t}{3}>0\Leftrightarrow \sin \frac{\pi t}{3}>0\)
Mà – 1 ≤ \(\frac{\pi t}{3}\)≤ 1 với mọi x ∈ ℝ. Do đó, \(0<\sin \frac{\pi t}{3}\le 1\).
+) v < 0 khi \(0,85\sin \frac{\pi t}{3}<0\Leftrightarrow \sin \frac{\pi t}{3}<0\).
Mà – 1 ≤ \(\frac{\pi t}{3}\)≤ 1 với mọi x ∈ ℝ. Do đó, −1 ≤ sin\(\frac{\pi t}{3}\) < 0.
+) Với t ∈ (0; 3) ta có 0 < sin\(\frac{\pi t}{3}\) ≤ 1.
+) Với t ∈ (3; 5] ta có −1 ≤ sin\(\frac{\pi t}{3}\) < 0.
Vậy trong khoảng thời gian từ 0 đến 5 giây, khoảng thời điểm sau 0 giây đến trước 3 giây thì người đó hít vào và khoảng thời điểm sau 3 giây đến 5 giây thì người đó thở ra.
Mục 3 trong SGK Toán 11 tập 1 - Kết nối tri thức tập trung vào việc nghiên cứu về giới hạn của hàm số tại một điểm. Đây là một khái niệm nền tảng quan trọng trong chương trình Toán học, mở đầu cho việc học về đạo hàm và tích phân trong các lớp học cao hơn. Việc hiểu rõ về giới hạn hàm số không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là bước đệm quan trọng để tiếp cận các kiến thức toán học phức tạp hơn.
Mục 3 bao gồm các nội dung chính sau:
a) lim (x→2) (x^2 + 3x - 1)
Để tính giới hạn này, ta có thể thay trực tiếp x = 2 vào biểu thức:
lim (x→2) (x^2 + 3x - 1) = 2^2 + 3*2 - 1 = 4 + 6 - 1 = 9
b) lim (x→-1) (x^3 - 2x + 5)
Tương tự, ta thay x = -1 vào biểu thức:
lim (x→-1) (x^3 - 2x + 5) = (-1)^3 - 2*(-1) + 5 = -1 + 2 + 5 = 6
a) lim (x→3) (x - 3) / (x^2 - 9)
Ta có thể phân tích mẫu số thành nhân tử:
lim (x→3) (x - 3) / (x^2 - 9) = lim (x→3) (x - 3) / ((x - 3)(x + 3)) = lim (x→3) 1 / (x + 3) = 1 / (3 + 3) = 1/6
b) lim (x→1) (x^2 - 1) / (x - 1)
Tương tự, ta phân tích tử số thành nhân tử:
lim (x→1) (x^2 - 1) / (x - 1) = lim (x→1) (x - 1)(x + 1) / (x - 1) = lim (x→1) (x + 1) = 1 + 1 = 2
Việc nắm vững kiến thức về giới hạn hàm số và rèn luyện kỹ năng giải bài tập là rất quan trọng đối với học sinh lớp 11. Hy vọng rằng, với lời giải chi tiết và các lưu ý trên, các em học sinh có thể tự tin giải quyết các bài tập về giới hạn hàm số trong SGK Toán 11 tập 1 - Kết nối tri thức và các bài tập khác.