Chào mừng bạn đến với bài học về lý thuyết định nghĩa và ý nghĩa của đạo hàm trong chương trình Toán 11 Kết nối tri thức. Đạo hàm là một khái niệm nền tảng quan trọng trong giải tích, mở ra cánh cửa để hiểu sâu hơn về sự thay đổi và tốc độ biến thiên của hàm số.
Bài viết này sẽ cung cấp cho bạn một cách tiếp cận toàn diện, từ định nghĩa cơ bản đến các ứng dụng thực tế, giúp bạn xây dựng nền tảng vững chắc cho các kiến thức toán học nâng cao hơn.
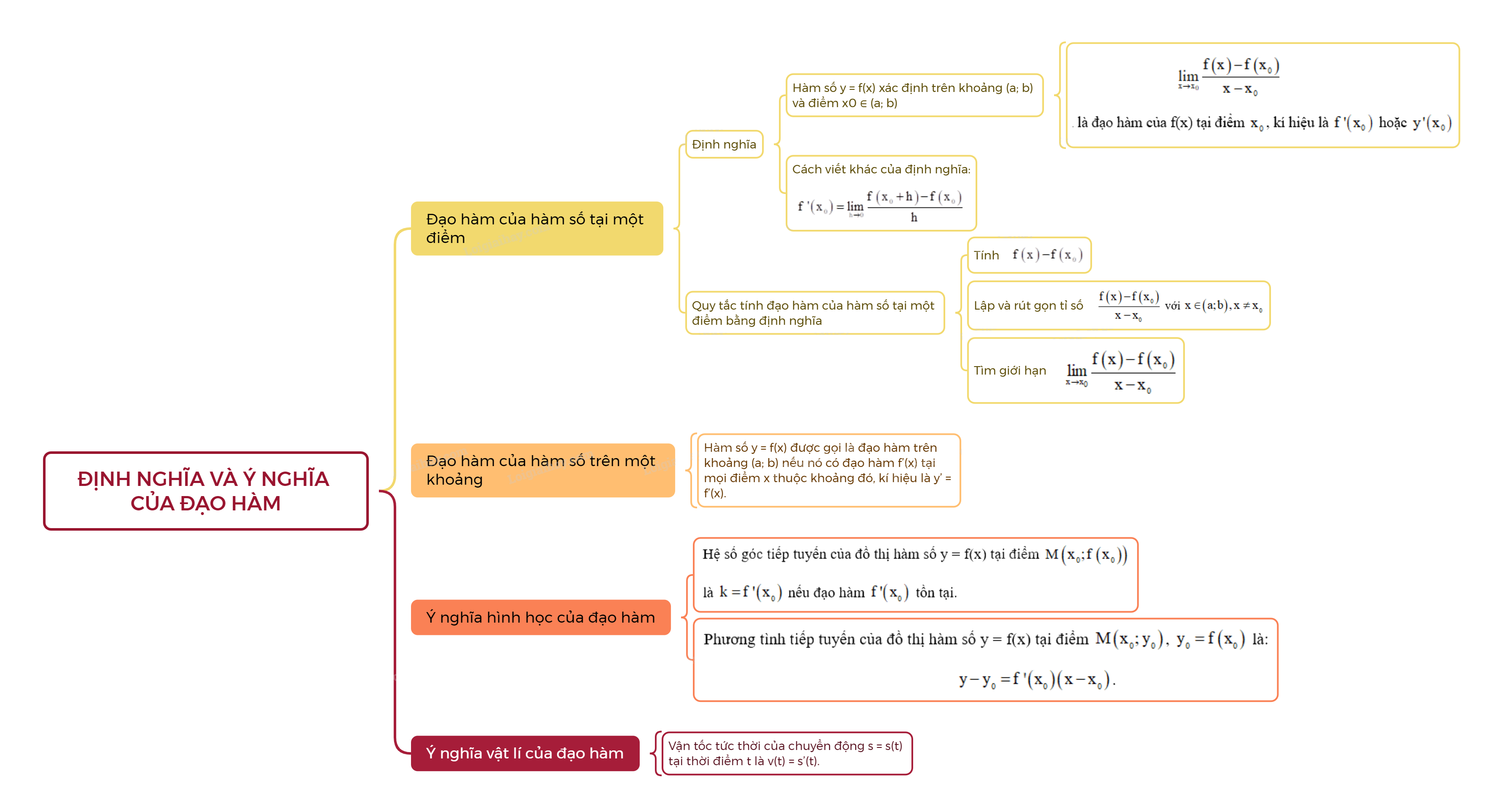
1. Đạo hàm của hàm số tại một điểm
1. Đạo hàm của hàm số tại một điểm
- Định nghĩa:Cho hàm số y = f(x) xác định trên khoảng \(\left( {a;b} \right)\) và điểm \({x_0} \in \left( {a;b} \right)\). Nếu tồn tại giới hạn (hữu hạn)
\(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\)
thì giới hạn đó được gọi là đạo hàm của f(x) tại điểm \({x_0}\), kí hiệu là \(f'\left( {{x_0}} \right)\) hoặc \(y'\left( {{x_0}} \right)\).
- Cách viết khác của định nghĩa:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {{x_0} + h} \right) - f\left( {{x_0}} \right)}}{h}\).
- Quy tắc tính đọa hàm của hàm số tại một điểm bằng định nghĩa:
Bước 1: Tính \(f\left( x \right) - f\left( {{x_0}} \right)\).
Bước 2: Lập và rút gọn tỉ số \(\frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) với \(x \in \left( {a;b} \right),x \ne {x_0}\).
Bước 3: Tìm giới hạn \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\).
2. Đạo hàm của hàm số trên một khoảng
Hàm số y = f(x) được gọi là đạo hàm trên khoảng (a; b) nếu nó có đạo hàm f’(x) tại mọi điểm x thuộc khoảng đó, kí hiệu là y’ = f’(x).
3. Ý nghĩa hình học của đạo hàm
- Hệ số góc tiếp tuyến của đồ thị hàm số y = f(x) tại điểm \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) là \(k = f'\left( {{x_0}} \right)\) nếu đạo hàm \(f'\left( {{x_0}} \right)\) tồn tại.
- Phương tình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm \(M\left( {{x_0};{y_0}} \right)\), \({y_0} = f\left( {{x_0}} \right)\) là:
\(y - {y_0} = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)\).
4. Ý nghĩa vật lí của đạo hàm
Vận tốc tức thời của chuyển động s = s(t) tại thời điểm t là v(t) = s’(t).
Đạo hàm là một khái niệm then chốt trong chương trình Toán 11 Kết nối tri thức, đóng vai trò quan trọng trong việc nghiên cứu sự biến thiên của hàm số và giải quyết các bài toán thực tế. Bài viết này sẽ trình bày chi tiết về định nghĩa, ý nghĩa và các tính chất cơ bản của đạo hàm.
Giả sử hàm số f(x) được xác định trên khoảng mở (a, b). Đạo hàm của f(x) tại điểm x0 thuộc (a, b) được định nghĩa là giới hạn:
f'(x0) = limh→0 [f(x0 + h) - f(x0)] / h
Nếu giới hạn này tồn tại, ta nói hàm số f(x) có đạo hàm tại x0. Ký hiệu f'(x0) còn được viết là df/dx hoặc d/dx f(x) khi x = x0.
Đạo hàm f'(x0) biểu thị hệ số góc của tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x0. Nói cách khác, đạo hàm cho biết độ dốc của đường cong tại một điểm cụ thể.
Nếu f'(x0) > 0, tiếp tuyến có độ dốc dương, hàm số đồng biến tại x0.
Nếu f'(x0) < 0, tiếp tuyến có độ dốc âm, hàm số nghịch biến tại x0.
Nếu f'(x0) = 0, tiếp tuyến song song với trục hoành, x0 là điểm cực trị của hàm số.
Trong vật lý, đạo hàm thường được sử dụng để biểu diễn vận tốc và gia tốc. Ví dụ, nếu s(t) là hàm biểu diễn quãng đường đi được của một vật tại thời điểm t, thì:
Để tính đạo hàm một cách hiệu quả, chúng ta cần nắm vững các quy tắc sau:
Ví dụ 1: Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1
f'(x) = (3x2)' + (2x)' - (1)' = 6x + 2 - 0 = 6x + 2
Ví dụ 2: Tính đạo hàm của hàm số g(x) = sin(x)
g'(x) = cos(x)
Đạo hàm có rất nhiều ứng dụng trong toán học và các lĩnh vực khác, bao gồm:
Để củng cố kiến thức, hãy thử giải các bài tập sau:
Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và đầy đủ về lý thuyết định nghĩa và ý nghĩa của đạo hàm trong chương trình Toán 11 Kết nối tri thức. Chúc bạn học tập tốt!