Bài 4.14 trang 82 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán liên quan đến quan hệ song song, vuông góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.14 trang 82 SGK Toán 11 tập 1, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD và P là một điểm thuộc cạnh AC. a) Xác định giao tuyến d của hai mặt phẳng (AMN) và (BPD) b) Chứng minh rằng d song song với BD
Đề bài
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD và P là một điểm thuộc cạnh AC.
a) Xác định giao tuyến d của hai mặt phẳng (AMN) và (BPD)
b) Chứng minh rằng d song song với BD
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Để xác định giao điểm của một đường thẳng và một mặt phẳng, ta có thể tìm giao điểm của đường thẳng đó với một đường thẳng nằm trong mặt phẳng đã cho.
Lời giải chi tiết
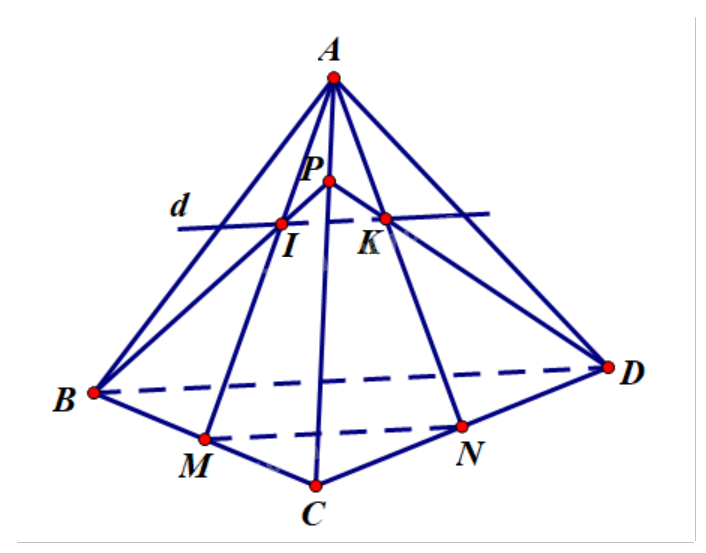
a) Gọi giao điểm của AM và BP là I, giao điểm của AN và DP là K.
Ta có IK đều thuộc mặt phẳng (AMN) và (BPD) suy ra IK là giao tuyến của hai mặt phẳng này.
Như vậy, d là đường thẳng đi qua I và K.
b) Ta có: \(mp\left( {AMN} \right) \cap mp\left( {BPD} \right) = IK\).
\(mp\left( {AMN} \right) \cap mp\left( {BCD} \right) = MN\) \(\;\).
\(mp\left( {BPD} \right) \cap mp\left( {BCD} \right) = BD\).
Mà MN // BD (do MN là đường trung bình của tam giác BCD) suy ra IK // BD.
Như vây, d song song với BD.
Bài 4.14 SGK Toán 11 tập 1 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về vị trí tương đối giữa đường thẳng và mặt phẳng. Để giải bài tập này, học sinh cần nắm vững các định nghĩa, tính chất và định lý liên quan đến đường thẳng song song, đường thẳng vuông góc với mặt phẳng, và hai mặt phẳng song song.
Bài tập yêu cầu chứng minh một số quan hệ về vị trí tương đối giữa đường thẳng và mặt phẳng dựa trên các giả thiết cho trước. Thông thường, bài tập sẽ cung cấp một hình chóp hoặc một hình đa diện và yêu cầu chứng minh một đường thẳng song song với một mặt phẳng, hoặc một đường thẳng vuông góc với một mặt phẳng.
Đề bài: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi M là trung điểm của CD. Chứng minh rằng SM vuông góc với mặt phẳng (ABCD).
Lời giải:
Bước 2: Chứng minh SM ⊥ (ABCD). Để chứng minh SM ⊥ (ABCD), ta cần chứng minh SM ⊥ AB và SM ⊥ BC.
Bước 3: Chứng minh SM ⊥ AB. Vì ABCD là hình vuông, AB ⊥ BC. Mặt khác, SM ⊥ (ABCD) nên SM ⊥ AB.
Bước 4: Chứng minh SM ⊥ BC. Vì ABCD là hình vuông, BC ⊥ AB. Mặt khác, SM ⊥ (ABCD) nên SM ⊥ BC.
Bước 5: Kết luận. Vì SM ⊥ AB và SM ⊥ BC, suy ra SM ⊥ (ABCD).
Để củng cố kiến thức và kỹ năng giải bài tập về vị trí tương đối giữa đường thẳng và mặt phẳng, học sinh có thể luyện tập thêm các bài tập tương tự trong SGK Toán 11 tập 1 Kết nối tri thức và các tài liệu tham khảo khác. Ngoài ra, học sinh cũng có thể tìm kiếm các bài giảng trực tuyến và các video hướng dẫn giải bài tập để hiểu rõ hơn về các khái niệm và phương pháp giải.
Bài 4.14 trang 82 SGK Toán 11 tập 1 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán về vị trí tương đối giữa đường thẳng và mặt phẳng. Bằng cách nắm vững các định lý, tính chất và phương pháp giải, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.