Bài 9.5 trang 86 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
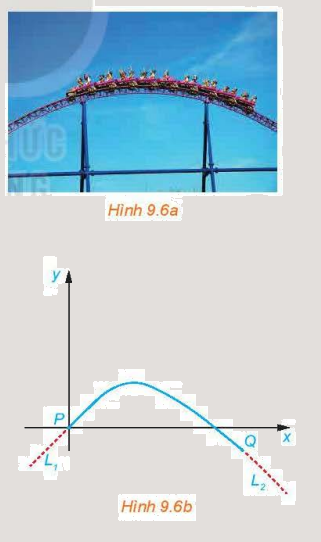
Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một cung đường cong có dạng parabol (H.9.6a)
Đề bài
Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một cung đường cong có dạng parabol (H.9.6a), đoạn dốc lên \({L_1}\) và đoạn dốc xuống \({L_2}\) là những phần đường thẳng có hệ số góc lần lượt là 0,5 và –0,75. Để tàu lượn chạy êm và không bị đổi hướng đột ngột, \({L_1}\) và \({L_2}\) phải là những tiếp tuyến của cung parabol tại các điểm chuyển tiếp P và Q (H.9.6b). Giả sử gốc toạ độ đặt tại P và phương trình của parabol là \(y = a{x^2} + bx + c,\) trong đó x tính bằng mét.
a) Tìm c.
b) Tính y'(0) và tìm b.
c) Giả sử khoảng cách theo phương ngang giữa P và Q là 40 m. Tìm a.
d) Tìm chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Hệ số góc của tiếp tuyến là \(f'\left( {{x_0}} \right)\)
Lời giải chi tiết
a) Vì gốc toạ độ đặt tại P nên P(0;0) do đó ta có c = y(0) = 0
b) \(y' = 2ax + b \Rightarrow y'\left( 0 \right) = b\)
Mà L1 là phương trình tiếp tuyến tại P có hệ số góc 0,5 nên \(y'\left( 0 \right) = 0,5 \Rightarrow b = 0,5\)
c) L2 là phương trình tiếp tuyến tại Q có hệ số góc – 0,75 nên \(y'\left( {{x_Q}} \right) = 2a{x_Q} + 0,5 = - 0,75\)
Vì khoảng cách theo phương ngang giữa P và Q là 40 m nên \({x_Q} - {x_P} = {x_Q} = 40\)
\( \Rightarrow 2a.40 + 0,5 = - 0,75 \Rightarrow a = \frac{{ - 1}}{{64}}\)
d) \({y_Q} = \frac{{ - 1}}{{64}}{.40^2} + 0,5.40 = - 5\)
Vậy chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q là \(\left| {{y_P} - {y_Q}} \right| = 5\)
Bài 9.5 trang 86 SGK Toán 11 tập 2 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức về đạo hàm, bao gồm đạo hàm của hàm số tại một điểm, đạo hàm của các hàm số cơ bản, và các quy tắc tính đạo hàm.
Bài tập 9.5 thường yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giải bài tập 9.5 trang 86 SGK Toán 11 tập 2 một cách hiệu quả, học sinh có thể áp dụng các phương pháp sau:
Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Tìm đạo hàm của hàm số và xác định khoảng đồng biến, nghịch biến của hàm số.
Giải:
Đạo hàm của hàm số y = x3 - 3x2 + 2 là:
y' = 3x2 - 6x
Để xác định khoảng đồng biến, nghịch biến, ta giải phương trình y' = 0:
3x2 - 6x = 0
⇔ 3x(x - 2) = 0
⇔ x = 0 hoặc x = 2
Ta xét dấu của y' trên các khoảng:
Vậy hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn khi giải các bài toán phức tạp.
Đạo hàm là một khái niệm quan trọng trong Toán học, có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau như Vật lý, Kinh tế, Kỹ thuật,... Việc nắm vững kiến thức về đạo hàm sẽ giúp học sinh hiểu sâu hơn về các hiện tượng tự nhiên và xã hội, đồng thời có thể giải quyết các bài toán thực tế một cách hiệu quả.
Giaitoan.edu.vn là một website học Toán online uy tín, cung cấp đầy đủ các bài giải chi tiết, dễ hiểu, giúp học sinh học Toán hiệu quả. Chúng tôi luôn cập nhật các bài giảng mới nhất, đáp ứng nhu cầu học tập của học sinh.