Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 3 trang 98 và 99 sách giáo khoa Toán 11 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Trong ba hình dưới đây, hình nào thể hiên hình lập phương chính xác hơn?
Video hướng dẫn giải
Trong ba hình dưới đây, hình nào thể hiên hình lập phương chính xác hơn?
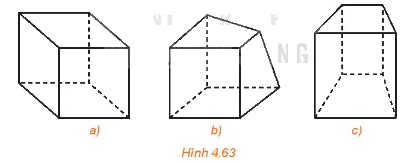
Phương pháp giải:
Hình lập phương là hình khối có chiều dài, chiều rộng và chiều cao đều bằng nhau. Hình lập phương có 6 mặt đều là hình vuông bằng nhau.
Lời giải chi tiết:
Hình a thể hiện hình lập phương chính xác hơn.
Video hướng dẫn giải
Vẽ hình biểu diễn của hình chóp S.ABCD có đáy ABCD là hình bình hành.
Phương pháp giải:
Hình biểu diễn của một hình trong không gian là hình chiếu song song của hình đó trên một mặt phẳng theo một phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.
Lời giải chi tiết:

Hình chóp S.ABCD có các mặt bên là hình tam giác nên hình biểu diễn của nó cũng có các mặt bên là hình tam giác.
ABCD là hình bình hành nên hình biểu diễn của nó cũng là hình bình hành
Từ đó, ta vẽ được hình biểu diễn của hình chóp S.ABCD
Video hướng dẫn giải
Phép chiếu song song có thể được sử dụng để vẽ dạng nổi (hay dạng 3D) của chữ cái như trong hình dưới đây. Theo phương pháp đó hãy vẽ dạng nổi của một số chữ cái quen thuộc như L, N, T,…
Phương pháp giải:
Hình chiếu bằng, hình chiếu đứng, hình chiếu cạnh của một vật thể là hình biểu diễn của vật thể đó.
Lời giải chi tiết:

Mục 3 của SGK Toán 11 tập 1 Kết nối tri thức tập trung vào các kiến thức về phép biến hình. Cụ thể, các em sẽ được làm quen với các khái niệm như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các phép biến hình này là nền tảng quan trọng để học tập các chương trình Toán học nâng cao hơn.
Phép tịnh tiến là một phép biến hình bảo toàn khoảng cách giữa hai điểm bất kỳ. Để thực hiện một phép tịnh tiến, ta cần xác định một vectơ tịnh tiến. Vectơ tịnh tiến này sẽ chỉ ra hướng và độ dài của phép tịnh tiến.
Công thức tổng quát của phép tịnh tiến là: M'(x'; y') = M(x; y) + v(a; b) trong đó M' là ảnh của điểm M qua phép tịnh tiến với vectơ v.
Phép quay là một phép biến hình bảo toàn khoảng cách giữa hai điểm bất kỳ và góc giữa hai đường thẳng bất kỳ. Để thực hiện một phép quay, ta cần xác định một tâm quay và một góc quay.
Công thức tổng quát của phép quay là: M'(x'; y') = O(x; y) + R(cos α; sin α) trong đó M' là ảnh của điểm M qua phép quay với tâm O và góc α.
Phép đối xứng trục là một phép biến hình biến mỗi điểm thành điểm đối xứng của nó qua một trục cho trước. Trục đối xứng này thường là đường thẳng.
Để tìm ảnh của một điểm M qua phép đối xứng trục d, ta cần tìm đường vuông góc từ M đến d và kéo dài đường này một khoảng bằng khoảng cách từ M đến d về phía bên kia của d.
Phép đối xứng tâm là một phép biến hình biến mỗi điểm thành điểm đối xứng của nó qua một tâm cho trước. Tâm đối xứng này thường là một điểm.
Để tìm ảnh của một điểm M qua phép đối xứng tâm O, ta cần tìm đường thẳng đi qua M và O, sau đó kéo dài đường này một khoảng bằng khoảng cách từ M đến O về phía bên kia của O.
Bài 1: Cho điểm A(1; 2) và vectơ tịnh tiến v(3; -1). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến theo vectơ v.
Lời giải: A'(x'; y') = A(x; y) + v(a; b) = (1; 2) + (3; -1) = (4; 1). Vậy A'(4; 1).
Bài 2: Cho điểm B(-2; 3) và tâm quay O(0; 0) với góc quay 90 độ. Tìm tọa độ điểm B' là ảnh của B qua phép quay tâm O với góc 90 độ.
Lời giải: B'(x'; y') = O(x; y) + R(cos 90°; sin 90°) = (-2; 3) + (0; 1) = (-2; 4). Vậy B'(-2; 4).
Phép biến hình có rất nhiều ứng dụng trong thực tế, chẳng hạn như trong thiết kế đồ họa, xây dựng, hàng không vũ trụ và nhiều lĩnh vực khác. Ví dụ, trong thiết kế đồ họa, phép biến hình được sử dụng để tạo ra các hiệu ứng đặc biệt, thay đổi kích thước và hình dạng của các đối tượng. Trong xây dựng, phép biến hình được sử dụng để tạo ra các mô hình 3D của các công trình. Trong hàng không vũ trụ, phép biến hình được sử dụng để điều khiển các tàu vũ trụ và vệ tinh.
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về mục 3 trang 98, 99 SGK Toán 11 tập 1 Kết nối tri thức. Chúc các em học tập tốt!