Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 4 trang 20 sách giáo khoa Toán 11 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và cập nhật nhất để hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng giaitoan.edu.vn khám phá lời giải chi tiết ngay sau đây!
Trong các công thức biến đổi tích thành tổng ở Mục 3, đặt \(u = a - b,\;v = a + b\) và viết các công thức nhận được
Trong các công thức biến đổi tích thành tổng ở Mục 3, đặt \(u = a - b,\;v = a + b\) và viết các công thức nhận được
Lời giải chi tiết:
Ta có: \(u = a - b;v = a + b\).
Suy ra \(u + v = 2a \to a = \frac{{u + v}}{2}\)
\(u - v = 2b \to b = \frac{{u - v}}{2}\)
Ta có: \(\cos u + \cos v = 2\cos \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\)
\(\cos u - \cos v = - 2\sin \frac{{u + v}}{2}\sin \frac{{u - v}}{2}\)
\(\sin u + \sin v = 2\sin \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\)
\(\sin u - \sin v = 2\cos \frac{{u + v}}{2}\sin \frac{{u - v}}{2}\)
Không dùng máy tính, tính giá trị của biểu thức
\(B = \cos \frac{\pi }{9} + \cos \frac{{5\pi }}{9} + \cos \frac{{11\pi }}{9}\).
Phương pháp giải:
Sử dụng công thức: \(\cos u + \cos v = 2\cos \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\)
Lời giải chi tiết:
\(B = \left( {\cos \frac{\pi }{9} + \cos \frac{{5\pi }}{9}} \right) + \cos \frac{{11\pi }}{9} = \left( {2\cos \frac{{\frac{\pi }{9} + \frac{{5\pi }}{9}}}{2}\cos \frac{{\frac{\pi }{9} - \frac{{5\pi }}{9}}}{2}} \right) + \cos \frac{{11\pi }}{9} = 2\cos \frac{\pi }{3}\cos \frac{{2\pi }}{9} + \cos \frac{{11\pi }}{9}\)
\( = \cos \frac{{2\pi }}{9} + \cos \frac{{11\pi }}{9} = 2\cos \frac{{\frac{{2\pi }}{9} + \frac{{11\pi }}{9}}}{2}\cos \frac{{\frac{{2\pi }}{9} - \frac{{11\pi }}{9}}}{2} = 2\cos \frac{{13\pi }}{{18}}\cos \frac{\pi }{2} = 0\)
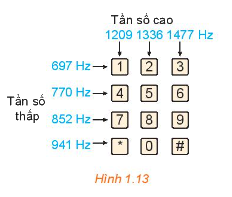
Khi nhấn một phím trên điện thoại cảm ứng, bàn phím sẽ tạo ra hai âm thuần, kết hợp với nhau để tạo ra âm thanh nhận dạng duy nhất phím. Hình 1.13 cho thấy tần số thấp \({f_1}\) và tần số cao \({f_2}\) liên quan đến mỗi phím. Nhấn một phím sẽ tạo ra sóng âm \(y = \sin \left( {2\pi {f_1}t} \right) + \sin \left( {2\pi {f_2}t} \right)\), ở đó t là biến thời gian (tính bằng giây).
a) Tìm hàm số mô hình hóa âm thanh được tạo ra khi nhấn phím 4.
b) Biến đổi công thức vừa tìm được ở câu a về dạng tích của một hàm số sin và một hàm số côsin.
Phương pháp giải:
Sử dụng công thức: \(\sin a + \sin b = 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\)
Lời giải chi tiết:
a) Khi nhấn phím 4, ta có sóng âm \(y = \sin \left( {2\pi .770t} \right) + \sin \left( {2\pi .1209t} \right)\)
b) Ta có: \(\sin \left( {2\pi .770t} \right) + \sin \left( {2\pi .1209t} \right) = 2\sin \frac{{2\pi .770t + 2\pi .1209t}}{2}\cos \frac{{2\pi .770t - 2\pi .1209t}}{2}\)
\( = - 2.\sin 1979\pi t.\sin 439\pi t\)
Mục 4 trang 20 SGK Toán 11 tập 1 - Kết nối tri thức thường xoay quanh các bài toán liên quan đến giới hạn của hàm số. Để giải quyết các bài toán này, học sinh cần nắm vững định nghĩa giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn thường gặp.
Giới hạn của hàm số f(x) khi x tiến tới a, ký hiệu là lim(x→a) f(x), là giá trị mà f(x) tiến tới khi x tiến gần a nhưng không bằng a. Định nghĩa này là nền tảng để hiểu và giải quyết các bài toán về giới hạn.
Các tính chất của giới hạn giúp đơn giản hóa quá trình tính toán giới hạn. Một số tính chất quan trọng bao gồm:
Có nhiều phương pháp để tính giới hạn, tùy thuộc vào dạng của hàm số. Một số phương pháp phổ biến bao gồm:
Bài toán: Tính lim(x→2) (x^2 - 4) / (x - 2)
Giải:
Ta có thể phân tích tử số thành nhân tử:
x^2 - 4 = (x - 2)(x + 2)
Vậy, lim(x→2) (x^2 - 4) / (x - 2) = lim(x→2) (x - 2)(x + 2) / (x - 2) = lim(x→2) (x + 2) = 2 + 2 = 4
Kết luận: lim(x→2) (x^2 - 4) / (x - 2) = 4
Để nắm vững kiến thức về giới hạn hàm số và rèn luyện kỹ năng giải bài tập, các em học sinh nên thực hành giải nhiều bài tập khác nhau. Giaitoan.edu.vn cung cấp một kho bài tập phong phú và đa dạng, giúp các em tự tin hơn trong quá trình học tập.
| Công thức | Mô tả |
|---|---|
| lim(x→a) c = c | Giới hạn của một hằng số bằng chính hằng số đó. |
| lim(x→a) x = a | Giới hạn của x khi x tiến tới a bằng a. |
| lim(x→a) (f(x) + g(x)) = lim(x→a) f(x) + lim(x→a) g(x) | Giới hạn của một tổng bằng tổng các giới hạn. |
| lim(x→a) (f(x) * g(x)) = lim(x→a) f(x) * lim(x→a) g(x) | Giới hạn của một tích bằng tích các giới hạn. |
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức hữu ích và phương pháp giải bài tập hiệu quả cho mục 4 trang 20 SGK Toán 11 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!