Chào mừng bạn đến với bài học về Lý thuyết Hai đường thẳng song song trong chương trình Toán 11 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hai đường thẳng song song, bao gồm định nghĩa, điều kiện nhận biết và các tính chất liên quan.
Chúng tôi tại giaitoan.edu.vn cam kết mang đến cho bạn trải nghiệm học tập trực tuyến hiệu quả và thú vị. Hãy cùng bắt đầu khám phá thế giới Toán học ngay bây giờ!
1. Vị trí tương đối của hai đường thẳng
1. Vị trí tương đối của hai đường thẳng
Cho hai đường thẳng a, b trong không gian.
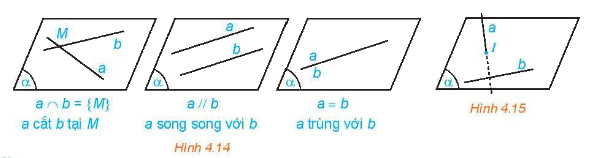
2. Tính chất của hai đường thẳng song song
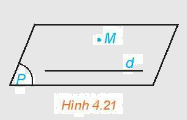
Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho.
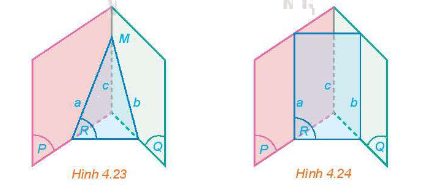
Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì song song với nhau.
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì 3 giao tuyến đó đồng quy hoặc đôi một song song.
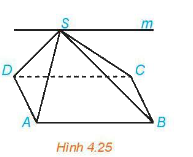
* Chú ý: Nếu hai mặt phẳng chứa 2 đường thẳng song song với nhau thì giao tuyến (nếu có) của chúng song song với 2 đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
VD: \(\left( {SAB} \right) \cap \left( {SBC} \right) = Sm\)

Trong chương trình Toán 11 Kết nối tri thức, kiến thức về hai đường thẳng song song đóng vai trò nền tảng cho việc hiểu và giải quyết các bài toán hình học không gian. Bài viết này sẽ trình bày chi tiết lý thuyết, các định lý, tính chất và ứng dụng của hai đường thẳng song song, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Hai đường thẳng được gọi là song song khi chúng không có điểm chung. Điều này có nghĩa là chúng không cắt nhau tại bất kỳ điểm nào trên mặt phẳng.
Có nhiều cách để xác định hai đường thẳng song song:
Hai đường thẳng song song có những tính chất quan trọng sau:
Có một số định lý quan trọng liên quan đến hai đường thẳng song song:
Lý thuyết hai đường thẳng song song được ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học và thực tế:
Bài tập 1: Cho hai đường thẳng d1 và d2 song song. Đường thẳng d3 cắt d1 tại A và d2 tại B. Tính góc ABd1 nếu góc d1AB = 60 độ.
Giải: Vì d1 và d2 song song, góc ABd1 bằng góc d1AB (hai góc đồng vị). Vậy góc ABd1 = 60 độ.
Bài tập 2: Cho hình thang ABCD với AB song song CD. Biết góc A = 80 độ, góc D = 100 độ. Tính góc B và góc C.
Giải: Vì AB song song CD, góc A + góc D = 180 độ (hai góc trong cùng phía). Tuy nhiên, 80 + 100 = 180 độ, điều này không đúng. Do đó, đề bài có thể có sai sót. Nếu góc D = 100 độ, thì góc C = 180 - 100 = 80 độ. Góc B = 180 - 80 = 100 độ.
Lý thuyết hai đường thẳng song song là một phần quan trọng của chương trình Toán 11 Kết nối tri thức. Việc nắm vững lý thuyết và các ứng dụng của nó sẽ giúp học sinh giải quyết các bài toán hình học một cách hiệu quả và chính xác. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn trong việc học tập.