Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 3 trang 107, 108 sách giáo khoa Toán 11 tập 1 chương trình Kết nối tri thức.
Bài viết này sẽ giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập về nhà.
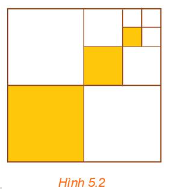
Cho hình vuông cạnh 1 (đơn vị độ dài). Chia hình vuông đó thành bốn hình vuông nhỏ bằng nhau, sau đó ô màu hình vuông nhỏ góc dưới bên trái (H.5.2). Lặp lại các thao tác này với hình vuông nhỏ góc trên bên phải. Giả sử quá trình trên tiếp diễn vô hạn lần. Gọi ({u_1},;{u_2}, ldots ,;{u_n}, ldots ) lần lượt là độ dài cạnh của các hình vuông được tô màu. a) Tính tổng ({S_n} = {u_1} + {u_2} + ldots + {u_n}) b) Tìm (S = mathop {lim}limits_{n to + infty } {S_n})
Video hướng dẫn giải
Cho hình vuông cạnh 1 (đơn vị độ dài). Chia hình vuông đó thành bốn hình vuông nhỏ bằng nhau, sau đó ô màu hình vuông nhỏ góc dưới bên trái (H.5.2). Lặp lại các thao tác này với hình vuông nhỏ góc trên bên phải. Giả sử quá trình trên tiếp diễn vô hạn lần. Gọi \({u_1},\;{u_2}, \ldots ,\;{u_n}, \ldots \) lần lượt là độ dài cạnh của các hình vuông được tô màu.
a) Tính tổng \({S_n} = {u_1} + {u_2} + \ldots + {u_n}\)
b) Tìm \(S = \mathop {lim}\limits_{n \to + \infty } {S_n}\)
Phương pháp giải:
Dựa vào đề bài để tìm ra biểu thức \({S_n}\). Sau đó tìm giới hạn.
Lời giải chi tiết:
Ta có: \({u_n} = \frac{1}{2} \times \frac{1}{{{2^{n - 1}}}}\).
a) \({S_n} = \frac{{\frac{1}{2} \times \left( {\frac{1}{{{2^n}}} - 1} \right)}}{{\frac{1}{2} - 1}} = 1 - \frac{1}{{{2^n}}}\).
b) \(S = \mathop {lim}\limits_{n \to + \infty } {S_n}= \mathop {lim}\limits_{n \to + \infty } \left( {1 - \frac{1}{{{2^n}}}} \right)\; = 1\).
Video hướng dẫn giải
Tính tổng \(S = 2 + \frac{2}{7} + \frac{2}{{7^2}} + \ldots + \frac{2}{{{7^{n - 1}}}} + \ldots \).
Phương pháp giải:
Dựa vào công thức tổng cấp số nhân lùi vô hạn \(S = \frac{{{u_1}}}{{1 - q}}\).
.
Lời giải chi tiết:
\(S = 2 + \frac{2}{7} + \frac{2}{{49}} + \ldots + \frac{2}{{{7^{n - 1}}}} + \ldots = 2 \times \left( {1 + \frac{1}{7} + \frac{1}{{49}} + \ldots + \frac{1}{{{7^{n - 1}}}} + \ldots } \right) = 2 \times \frac{1}{{1 - \frac{1}{7}}} = \frac{7}{3}\).
Video hướng dẫn giải
Để đơn giản, ta giả sử Achilles chạy với vận tốc 100km.h, vận tốc của rùa là 1 km/h và khoảng cách ban đầu a = 100(km)
a) Tính thời gian \({t_1},\;{t_2}, \ldots ,{t_n}, \ldots \) tương ứng để Achilles đi từ \({A_1}\) đến \({A_2}\), từ \({A_2}\) đến \({A_3}\),…, từ \({A_n}\) đến \({A_{n + 1}}\),…
b) Tính tổng thời gian cần thiết để Achilles chạy hết các quãng đường \({A_1}{A_2},\;{A_2}{A_3}, \ldots ,\;{A_n}{A_{n + 1}}\),… tức là thời gian cần thiết để Achilles đuổi kịp rùa
c) Sai lầm trong lập luận của Zeno là ở đâu?
Phương pháp giải:
Để tính tổng thời gian chạy hết quãng đường, ta sử dụng công thức tổng cấp số nhân lùi vô hạn
Lời giải chi tiết:
Ta có: Achilles chạy với vận tốc 100km/h, vận tốc của rùa là 1 km/h.
a) Để chạy hết quãng đường từ \({A_1}\) đến \({A_2}\) với \({A_1}{A_2} = a = 100\)(km), Achilles phải mất thời gian \({t_1} = \frac{{100}}{{100}} = 1(h)\). Với thời gian \({t_1}\)này, rùa đã chạy được quãng đường \({A_2}{A_3} = 1(km)\).
Để chạy hết quãng đường từ \({A_2}\)đến \({A_3}\)với \({A_2}{A_3} = 1(km)\), Achilles phải mất thời gian \({t_2} = \frac{1}{{100}}(h)\). Với thời gian \({t_2}\)này, rùa đã chạy được quãng đường \({A_3}{A_4} = \frac{1}{{100}}(km)\)
Để chạy hết quãng đường từ \({A_n}\)đến \({A_{n + 1}}\)với \({A_n}{A_{n + 1}} = \frac{1}{{{{100}^{ - 2}}}}(km)\), Achilles phải mất thời gian \({t_n} = \frac{1}{{{{100}^{n - 1}}}}(h)\).
b) Tổng thời gian cần thiết để chạy hết quãng đường từ \({A_1}{A_2},{A_2}{A_3},...,{A_n}{A_{n + 1}},...\)tức là thời gian cần thiết để Achilles đuổi kịp rùa là:
\(T = 1 + \frac{1}{{100}} + \frac{1}{{{{100}^2}}} + ... + \frac{1}{{{{100}^{n - 1}}}} + \frac{1}{{{{100}^n}}} + ...(h)\)
Đó là tổng của một cấp số nhân lùi vô hạn với \({u_1} = 1,q = \frac{1}{{100}}\), nên ta có:
\(T = \frac{{{u_1}}}{{1 - q}} = \frac{1}{{1 - \frac{1}{{100}}}} = \frac{{100}}{{99}} = 1\frac{1}{{99}}(h)\)
Như vậy, Achilles đuổi kịp rùa sau: \(1\frac{1}{{99}}(h)\)
c) Nghịch lý Zeno chỉ đúng với điều kiện là tổng thời gian Achilles chạy hết các quãng đường để đuổi kịp rùa phải là vô hạn, còn nếu nó hữu hạn thì đó chính là khoảng thời gian mà anh bắt kịp được rùa
Mục 3 trong SGK Toán 11 tập 1 Kết nối tri thức tập trung vào việc nghiên cứu về phép biến hình affine. Đây là một khái niệm quan trọng trong hình học, mở rộng phạm vi nghiên cứu từ các phép biến hình đơn giản như phép tịnh tiến, phép quay, phép đối xứng đến các phép biến hình phức tạp hơn. Việc hiểu rõ về phép biến hình affine giúp học sinh có cái nhìn sâu sắc hơn về mối quan hệ giữa các đối tượng hình học và ứng dụng của chúng trong thực tế.
Mục 3 bao gồm các nội dung chính sau:
Bài tập này yêu cầu học sinh xác định một phép biến hình affine dựa trên các thông tin cho trước. Để giải bài tập này, học sinh cần nắm vững định nghĩa của phép biến hình affine và cách xác định một phép biến hình affine thông qua các điểm ảnh của nó.
Ví dụ, cho hai điểm A(1, 2) và B(3, 4) và ảnh của chúng qua phép biến hình affine f là A'(2, 3) và B'(4, 5). Hãy xác định phép biến hình affine f.
Lời giải: Gọi ma trận của phép biến hình affine f là M = [[a, b], [c, d]]. Ta có:
M * [1, 2] = [2, 3] và M * [3, 4] = [4, 5]
Giải hệ phương trình này, ta tìm được a, b, c, d và xác định được ma trận M của phép biến hình affine f.
Bài tập này yêu cầu học sinh tìm ma trận của một phép biến hình affine dựa trên các thông tin cho trước. Để giải bài tập này, học sinh cần nắm vững cách biểu diễn một phép biến hình affine bằng ma trận và cách tính toán ma trận của phép biến hình affine.
Ví dụ, cho phép biến hình affine f là phép tịnh tiến theo vectơ v = (1, 2). Hãy tìm ma trận của phép biến hình affine f.
Lời giải: Ma trận của phép tịnh tiến theo vectơ v = (1, 2) là:
M = [[1, 0, 1], [0, 1, 2], [0, 0, 1]]
Bài tập này yêu cầu học sinh ứng dụng kiến thức về phép biến hình affine để giải quyết các bài toán thực tế. Để giải bài tập này, học sinh cần hiểu rõ các ứng dụng của phép biến hình affine và cách sử dụng phép biến hình affine để giải quyết các bài toán cụ thể.
Ví dụ, cho một hình vuông ABCD có tọa độ A(0, 0), B(1, 0), C(1, 1), D(0, 1). Hãy tìm ảnh của hình vuông ABCD qua phép biến hình affine f là phép quay quanh gốc tọa độ O một góc 90 độ.
Lời giải: Ma trận của phép quay quanh gốc tọa độ O một góc 90 độ là:
M = [[0, -1], [1, 0]]
Áp dụng phép biến hình affine f lên các đỉnh của hình vuông ABCD, ta tìm được tọa độ của các đỉnh A', B', C', D' và vẽ lại hình vuông A'B'C'D'.
Để học tốt mục 3, các em nên:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức hữu ích về phép biến hình affine và giúp các em giải quyết thành công các bài tập trong SGK Toán 11 tập 1 Kết nối tri thức. Chúc các em học tập tốt!