Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 46, 47 SGK Toán 11 tập 2 chương trình Kết nối tri thức. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập mục 3 tập trung vào các kiến thức quan trọng về...
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau.
Video hướng dẫn giải
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Kẻ đường thẳng a thuộc (P) và vuông góc với giao tuyến \(\Delta \) của (P) và (Q). Gọi O là giao điểm của a và \(\Delta \). Trong mặt phẳng (Q), gọi b là đường thẳng vuông góc với \(\Delta \) tại O.
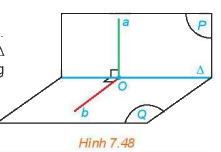
a) Tính góc giữa a và b.
b) Tìm mỗi quan hệ giữa a và (Q).
Phương pháp giải:
- Sử dụng nhận xét trang 45 để xác định góc giữa 2 mặt phẳng.
- Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.
Lời giải chi tiết:
a) \(\left\{ \begin{array}{l}(P) \cap (Q) = \Delta \\a \subset (P),a \bot \Delta \\b \subset (Q),b \bot \Delta \end{array} \right. \Rightarrow \left( {(P),(Q)} \right) = \left( {a,b} \right)\)
Do \((P) \bot (Q) \Rightarrow \left( {(P),(Q)} \right) = {90^0} \Rightarrow \left( {a,b} \right) = {90^0}\)
b) Do \(\left\{ \begin{array}{l}a \bot b\\a \bot \Delta \\b \cap \Delta \end{array} \right. \Rightarrow a \bot (Q)\)
Video hướng dẫn giải
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến a và cùng vuông góc với mặt phẳng (R). Gọi O là một điểm thuộc a và a' là đường thẳng qua O và vuông góc với (R).

a) Hỏi a' có nằm trong các mặt phẳng (P), (Q) hay không?
b) Tìm mối quan hệ giữa a và a'.
c) Tìm mối quan hệ giữa a và (R).
Phương pháp giải:
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Mỗi đường thẳng qua điểm O thuộc (P) và vuông góc với mặt phẳng (Q) thì đường thẳng đó thuộc mặt phẳng (P).
Lời giải chi tiết:
a) Vì O là một điểm thuộc a là giao tuyến của hai mặt phẳng (P), (Q) và a' là đường thẳng qua O và vuông góc với (R).
Theo nhận xét trang 46 thì a' có nằm trong các mặt phẳng (P), (Q).
b) Vì a' có nằm trong các mặt phẳng (P), (Q) nên a’ là giao tuyến của hai mặt phẳng (P), (Q) do đó a trùng a' (do a cũng là giao tuyến của hai mặt phẳng (P), (Q)).
c) a vuông góc với (R) do a trùng a’ và a’ vuông góc với (R).
Video hướng dẫn giải
Với giả thiết như ở Ví dụ 3, chứng minh rằng:
a) Các mặt phẳng (AB'C'D') và (ABCD) cùng vuông góc với (SAC);
b) Giao tuyển của hai mặt phẳng (AB'C'D') và (ABCD) là đường thẳng đi qua A, nằm trong mặt phẳng (ABCD) và vuông góc với AC.
Phương pháp giải:
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.
Lời giải chi tiết:

a) Từ ví dụ 3b ta có AB’, AC’ cùng đi qua A và vuông góc với SC
\( \Rightarrow SC \bot \left( {AB'C'D'} \right),SC \subset \left( {SAC} \right) \Rightarrow \left( {AB'C'D'} \right) \bot \left( {SAC} \right)\)
Ta có \(SA \bot \left( {ABCD} \right),SA \subset \left( {SAC} \right) \Rightarrow \left( {ABCD} \right) \bot \left( {SAC} \right)\)
Do đó các mặt phẳng (AB'C'D') và (ABCD) cùng vuông góc với (SAC).
b) Vì (AB'C'D') và (ABCD) cùng vuông góc với (SAC) nên giao tuyến của hai mặt phẳng (AB'C'D') và (ABCD) vuông góc với (SAC)
Vậy giao tuyển của hai mặt phẳng (AB'C'D') và (ABCD) là đường thẳng đi qua A, nằm trong mặt phẳng (ABCD) và vuông góc với AC.
Mục 3 trang 46, 47 SGK Toán 11 tập 2 Kết nối tri thức là một phần quan trọng trong chương trình học, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Để giúp các em học sinh hiểu rõ hơn về nội dung này, giaitoan.edu.vn xin trình bày chi tiết lời giải các bài tập trong mục này.
Mục 3 thường bao gồm các dạng bài tập liên quan đến... (Ví dụ: ứng dụng của đạo hàm để khảo sát hàm số, tìm cực trị, giải phương trình, bất phương trình,...). Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để hoàn thành tốt các bài tập này.
Đề bài: (Ví dụ: Cho hàm số y = f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.)
Lời giải:
Đề bài: (Ví dụ: Giải phương trình x3 - 3x + 2 = 0)
Lời giải:
Đề bài: (Ví dụ: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x2 - 4x + 3 trên đoạn [-1; 3])
Lời giải:
...
Kiến thức về đạo hàm và ứng dụng của đạo hàm có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học kỹ thuật, như:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập mục 3 trang 46, 47 SGK Toán 11 tập 2 Kết nối tri thức mà giaitoan.edu.vn cung cấp, các em học sinh sẽ hiểu rõ hơn về nội dung này và đạt kết quả tốt trong học tập. Chúc các em học tốt!