Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 54 và 55 sách giáo khoa Toán 11 tập 2, chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
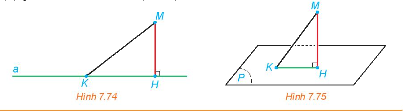
a) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, vì sao MK ≥ MH (H.7.74)
Video hướng dẫn giải
a) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, vì sao MK ≥ MH (H.7.74)
b) Cho điểm M và mặt phẳng (P). Gọi H là hình chiếu của M trên (P). Với mỗi điểm K thuộc (P), giải thích vì sao MK ≥ MH (H.7.75).
Phương pháp giải:
Dựa vào mối quan hệ đường xiên và đường vuông góc.
Lời giải chi tiết:
a) Vì H là hình chiếu của M trên đường thẳng a, nên MH là khoảng cách từ M đến a và MH là đoạn thẳng ngắn nhất từ M đến a, suy ra MK ≥ MH.
b) Vì H là hình chiếu của M trên (P) nên MH vuông góc với (P) do đó MH vuông góc với HK.
Dựa vào mối quan hệ đường xiên và đường vuông góc ta có MK ≥ MH.
Video hướng dẫn giải
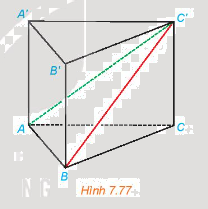
Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân tại A, AB = a, AA' = h (H.7.77).
a) Tính khoảng cách từ A đến mặt phẳng (BCC'B').
b) Tam giác ABC' là tam giác gì? Tính khoảng cách từ A đến BC'.

Phương pháp giải:
- Khoảng cách từ một điểm M đến một đường thẳng a, kí hiệu d (M, a), là khoảng cách giữa M và hình chiếu H của M trên a.
- Khoảng cách từ một điểm M đến một mặt phẳng (P), kí hiệu d (M, (P)), là khoảng cách giữa M và hình chiếu H của M trên (P).
Lời giải chi tiết:
a) Ta có \(BB' \bot \left( {ABC} \right);BB' \subset \left( {BCC'B'} \right) \Rightarrow \left( {ABC} \right) \bot \left( {BCC'B'} \right)\)
\(\left( {ABC} \right) \cap \left( {BCC'B'} \right) = BC\)
(ABC): Kẻ \(AH \bot BC\)
\( \Rightarrow AH \bot \left( {BCC'B'} \right) \Rightarrow d\left( {A,\left( {BCC'B'} \right)} \right) = AH\)
Xét tam giác ABC vuông cân tại A có
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{2}{{{a^2}}}\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow AH = \frac{{a\sqrt 2 }}{2}\)
b) +) Ta có \(AB \bot AC,AB \bot AA'\left( {AA' \bot \left( {ABC} \right)} \right) \Rightarrow AB \bot \left( {ACC'A'} \right);AC' \subset \left( {ACC'A'} \right) \Rightarrow AC' \bot AB\)
Do đó tam giác ABC' là tam giác vuông.
+) Trên (ABC’) kẻ \(AK \bot BC' \Rightarrow d\left( {A,BC'} \right) = AK\)
Xét tam giác ACC’ vuông tại C có
\(A{C'^2} = A{C^2} + C{C'^2} = {a^2} + {h^2}\) (Định lí Pytago)
Xét tam giác ABC’ vuông tại A có
\(\begin{array}{l}\frac{1}{{A{K^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{{C'}^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2} + {h^2}}} = \frac{{2{a^2} + {h^2}}}{{{a^2}\left( {{a^2} + {h^2}} \right)}} \Rightarrow A{K^2} = \frac{{{a^2}\left( {{a^2} + {h^2}} \right)}}{{2{a^2} + {h^2}}}\\ \Rightarrow AK = a.\sqrt {\frac{{{a^2} + {h^2}}}{{2{a^2} + {h^2}}}} \end{array}\)
Mục 1 của chương trình Toán 11 tập 2, Kết nối tri thức, tập trung vào việc ôn tập và mở rộng kiến thức về đạo hàm. Các bài tập trang 54 và 55 SGK Toán 11 tập 2 yêu cầu học sinh vận dụng các quy tắc tính đạo hàm đã học để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và công thức đạo hàm là nền tảng quan trọng để giải quyết thành công các bài tập này.
Bài tập này yêu cầu học sinh tính đạo hàm của các hàm số đơn thức, đa thức và các hàm số có dạng tổng, hiệu, tích, thương. Để giải bài tập này, học sinh cần áp dụng các quy tắc tính đạo hàm của tổng, hiệu, tích, thương và quy tắc đạo hàm của hàm số lũy thừa.
Bài tập này yêu cầu học sinh tìm đạo hàm của các hàm số phức tạp hơn, bao gồm các hàm số hợp và các hàm số lượng giác. Để giải bài tập này, học sinh cần áp dụng quy tắc đạo hàm của hàm số hợp và các quy tắc tính đạo hàm của các hàm số lượng giác.
Bài tập này yêu cầu học sinh tính đạo hàm cấp hai của các hàm số đã cho. Đạo hàm cấp hai là đạo hàm của đạo hàm cấp một. Để giải bài tập này, học sinh cần tính đạo hàm cấp một trước, sau đó tính đạo hàm của đạo hàm cấp một để được đạo hàm cấp hai.
Ví dụ 1: Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1.
Giải:
f'(x) = (3x2)' + (2x)' - (1)' = 6x + 2 - 0 = 6x + 2.
Ví dụ 2: Tính đạo hàm của hàm số g(x) = sin(x) * cos(x).
Giải:
g'(x) = (sin(x))' * cos(x) + sin(x) * (cos(x))' = cos(x) * cos(x) + sin(x) * (-sin(x)) = cos2(x) - sin2(x).
Việc giải các bài tập trong mục 1 trang 54, 55 SGK Toán 11 tập 2 - Kết nối tri thức là một bước quan trọng trong quá trình học tập môn Toán của các em. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải quyết các bài toán đạo hàm và đạt kết quả tốt nhất.