Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 67, 68 sách giáo khoa Toán 11 tập 2 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Một tổ trong lớp 11A có 10 học sinh. Điểm kiểm tra học kì I của 10 bạn này ở hai môn Toán và Ngữ văn được cho như sau:
Video hướng dẫn giải
Một tổ trong lớp 11A có 10 học sinh. Điểm kiểm tra học kì I của 10 bạn này ở hai môn Toán và Ngữ văn được cho như sau:
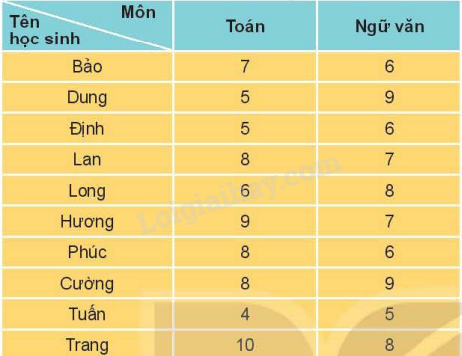
Chọn ngẫu nhiên một học sinh trong tổ. Xét các biến cố sau:
A: “Học sinh đó được điểm giỏi môn Ngữ văn”;
B: “Học sinh đó được điểm giỏi môn Toán”;
C: “Học sinh đó được điểm giỏi môn Ngữ văn hoặc điểm giỏi môn Toán”.
a) Mô tả không gian mẫu và các tập con A, B, C của không gian mẫu.
b) Tìm \(A \cup B\)
Phương pháp giải:
Dựa vào đề bài để liệt kê
Lời giải chi tiết:
a) A = {Dung, Long, Cường, Trang}
B = {Lan, Hương, Phúc, Cường, Trang}
C = {Dung, Long, Lan, Hương, Phúc, Cường, Trang}
b) \(A \cup B\) = {Dung, Long, Cường, Trang, Lan, Hương, Phúc}
Video hướng dẫn giải
Một tổ trong lớp 11B có 4 học sinh nữ là Hương, Hồng, Dung, Phương và 5 học sinh nam là Sơn, Tùng, Hoàng, Tiến, Hải. Trong giờ học, giáo viên chọn ngẫu nhiên một học sinh trong tổ đó lên bảng để kiểm tra bài. Xét các biến cố sau:
H: “Học sinh đó là một bạn nữ”;
K: “Học sinh đó có tên bắt đầu là chữ cái H”.
a) Mô tả không gian mẫu.
b) Nêu nội dung của biến cố hợp \(M = H \cup K.\) Mỗi biến cố H, K, M là tập con nào của không gian mẫu?
Phương pháp giải:
Cho A và B là hai biến cố. Biến cố: “A hoặc B xảy ra” được gọi là biến cố hợp của A và B, kí hiệu là \(A \cup B.\)
Lời giải chi tiết:
a) Không gian mẫu của bài toán này là tập hợp các học sinh trong tổ lớp, nó có 9 phần tử và được ký hiệu là Ω = {Hương, Hồng, Dung, Phương, Sơn, Tùng, Hoàng, Tiến, Hải}.
b) Biến cố H xảy ra khi học sinh được chọn là một bạn nữ, nó là tập hợp các học sinh nữ và được ký hiệu là
H = {Hương, Hồng, Dung, Phương}.
Biến cố K xảy ra khi học sinh được chọn có tên bắt đầu là chữ cái H, được ký hiệu là
K = {Hương, Hồng, Hoàng, Hải}.
Biến cố hợp M xảy ra khi học sinh được chọn là một bạn nữ hoặc có tên bắt đầu bằng chữ H, nó là tập hợp các học sinh trong tập H hoặc K (bao gồm cả những học sinh trùng nhau của hai tập này) và được ký hiệu là
\(M = H \cup K\) = {Hương, Hồng, Dung, Phương, Hoàng, Hải}.
Mục 1 của chương trình Toán 11 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa kiến thức về đạo hàm. Các bài tập trang 67 và 68 SGK Toán 11 tập 2 yêu cầu học sinh vận dụng các công thức, quy tắc đạo hàm đã học để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng tính toán là yếu tố then chốt để hoàn thành tốt các bài tập này.
Bài tập này yêu cầu học sinh tính đạo hàm của các hàm số đơn thức, đa thức, và các hàm số có dạng tổng, hiệu, tích, thương. Để giải bài tập này, học sinh cần áp dụng các quy tắc đạo hàm cơ bản như quy tắc đạo hàm của tổng, hiệu, tích, thương, và quy tắc đạo hàm của hàm hợp.
Bài tập này yêu cầu học sinh tính đạo hàm của các hàm số lượng giác, hàm mũ, hàm logarit. Để giải bài tập này, học sinh cần áp dụng các công thức đạo hàm của các hàm số lượng giác, hàm mũ, hàm logarit.
Ví dụ:
Bài tập này yêu cầu học sinh tìm đạo hàm cấp hai của các hàm số đã cho. Để giải bài tập này, học sinh cần tính đạo hàm cấp một trước, sau đó tính đạo hàm của đạo hàm cấp một để được đạo hàm cấp hai.
Ví dụ 1: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1
Giải:
f'(x) = (x3)' + (2x2)' - (5x)' + (1)' = 3x2 + 4x - 5 + 0 = 3x2 + 4x - 5
Ví dụ 2: Tính đạo hàm của hàm số g(x) = sin(2x)
Giải:
g'(x) = (sin(2x))' = cos(2x) * (2x)' = 2cos(2x)
Để củng cố kiến thức và kỹ năng giải bài tập đạo hàm, các em có thể luyện tập thêm với các bài tập tương tự trong SGK Toán 11 tập 2 - Kết nối tri thức và các tài liệu tham khảo khác.
Việc giải bài tập mục 1 trang 67, 68 SGK Toán 11 tập 2 - Kết nối tri thức đòi hỏi sự nắm vững kiến thức về đạo hàm và kỹ năng vận dụng các quy tắc đạo hàm một cách linh hoạt. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải quyết các bài tập này và đạt kết quả tốt trong môn Toán.