Bài 4.5 trang 77 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho hình chóp tứ giác S.ABCD và lấy một điểm E thuộc cạnh SA của hình chóp (E khác S, A).Trong mặt phẳng (ABCD) vẽ một đường thằng d cắt các cạnh CB, CD lần lượt tại M, N và cắt các tia AB, AD lần lượt tại P, Q.
Đề bài
Cho hình chóp tứ giác S.ABCD và lấy một điểm E thuộc cạnh SA của hình chóp (E khác S, A).Trong mặt phẳng (ABCD) vẽ một đường thằng d cắt các cạnh CB, CD lần lượt tại M, N và cắt các tia AB, AD lần lượt tại P, Q.
a) Xác định giao điểm của mp (E,d) với các cạnh SB, SD của hình chóp.
b) Xác định giao tuyến của mp (E,d) với các mặt của hình chóp.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Để xác định giao điểm của một đường thẳng và một mặt phẳng, ta có thể tìm giao điểm của đường thẳng đó với một đường thẳng nằm trong mặt phẳng đã cho.
Để chứng minh giao tuyến của hai mặt phẳng, ta tìm hai điểm cùng thuộc cả hai mặt phẳng đó.
Lời giải chi tiết
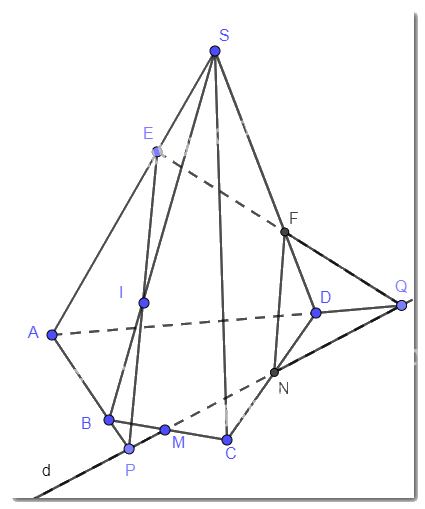
a)
- Giao điểm của mp(E,d) với cạnh SB
P thuộc AB suy ra P cũng thuộc mp(SAB)
Trên mp(SAB), gọi giao điểm của EP và SB là I
P thuộc đường thẳng d suy ra P cũng nằm trên mp(E,d)
E, P đều nằm trên mp(D,d) suy ra EP nằm trên mp(E,d) suy ra I cũng nằm trên mp(E,d)
Vậy I là giao điểm của mp(E,d) và SB
- Giao điểm của mp(E,d) với cạnh SD.
Q thuộc AD suy ra Q nằm trên mp(SAD)
Gọi giao điểm của EQ và SD là F
Q thuộc đường thẳng d suy ra Q cũng nằm trên mp(E,d)
E, Q đều nằm trên mp(E,d) suy ra EQ nằm trên mp(E,d) , suy ra F cũng nằm trên mp(E,d)
Vậy F là giao điểm của mp(E,d) và SD.
b) Ta có EI cùng thuộc mp(SAB) và mp(E,d) suy ra EI là tuyến điểm của hai mặt phẳng.
EF cùng thuộc mp(SAD) và mp(E,d) suy ra EF là giao tuyến của hai mặt phẳng
\(IM \subset mp\left( {SBC} \right),IM \subset mp\left( {E,d} \right)\) suy ra IM là giao tuyến của hai mp(SBC) và mp(E,d).
\(FN \subset mp\left( {SCD} \right),FN \subset mp\left( {E,d} \right)\) suy ra FN là giao tuyến của mp(SCD) và mp(E,d).
Bài 4.5 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của hàm số. Bài tập này thường xuất hiện trong các đề thi và kiểm tra, do đó việc nắm vững phương pháp giải là rất cần thiết.
Bài 4.5 thường yêu cầu học sinh:
Để giải bài 4.5 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức, học sinh cần:
Ví dụ 1: Cho hàm số f(x) = x2 + 2x + 1. Tính f'(3).
Giải:
f'(x) = 2x + 2
f'(3) = 2(3) + 2 = 8
Ví dụ 2: Tìm hệ số góc của tiếp tuyến với đồ thị hàm số y = x3 - 3x + 2 tại điểm có hoành độ x = 1.
Giải:
y' = 3x2 - 3
Hệ số góc của tiếp tuyến tại x = 1 là y'(1) = 3(1)2 - 3 = 0
Để củng cố kiến thức và kỹ năng giải bài tập, học sinh có thể tự giải các bài tập sau:
Khi giải bài tập về đạo hàm, học sinh cần chú ý:
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài 4.5 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về đạo hàm và ứng dụng của nó trong thực tế. Việc luyện tập thường xuyên và nắm vững phương pháp giải sẽ giúp học sinh đạt kết quả tốt trong môn Toán 11.
| Công thức | Mô tả |
|---|---|
| (xn)' = nxn-1 | Đạo hàm của hàm lũy thừa |
| (sin x)' = cos x | Đạo hàm của hàm sin |
| (cos x)' = -sin x | Đạo hàm của hàm cos |