Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 76 và 77 sách giáo khoa Toán 11 tập 2, chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Có hai hộp đựng các quả bóng có cùng kích thước và khối lượng. Hộp I có 6 quả màu trắng và 4 quả màu đen.
Video hướng dẫn giải
Có hai hộp đựng các quả bóng có cùng kích thước và khối lượng. Hộp I có 6 quả màu trắng và 4 quả màu đen. Hộp II có 1 quả màu trắng và 7 quả màu đen. Bạn Long lấy ngẫu nhiên một quả bóng từ hộp I, bạn Hải lấy ngẫu nhiên một quả bóng từ hộp II. Xét các biến cố sau:
A: “Bạn Long lấy được quả bóng màu trắng”;
B: “Bạn Hải lấy được quả bóng màu đen”.
a) Tính P(A), P(B) và P(AB).
b) So sánh P(AB) và P(A).P(B).
Phương pháp giải:
- \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\)
- Cho A và B là hai biến cố. Biến cố: “Cả A và B đều xảy ra” được gọi là biến cố giao của A và B, kí hiệu AB
Lời giải chi tiết:
a) \(P\left( A \right) = \frac{6}{{10}} = \frac{3}{5};P\left( B \right) = \frac{7}{8}\)
Không gian mẫu là tập hợp số cách Bạn Long lấy được một quả bóng từ hộp I và Bạn Hải lấy một quả bóng từ hộp II do đó \(n\left( \Omega \right) = 10.8 = 80\)
C: “Bạn Long lấy được quả màu trắng và bạn Hải lấy được quả màu đen”
Công đoạn 1: Bạn Long lấy được quả màu trắng có 6 cách
Công đoạn 2. Bạn Hải lấy được quả màu đen có 7 cách
Theo quy tắc nhân, tập hợp C có 6.7 = 42 (phần tử)
\(P\left( C \right) = P\left( {AB} \right) = \frac{{n\left( C \right)}}{{n\left( \Omega \right)}} = \frac{{42}}{{80}} = \frac{{21}}{{40}}\)
b) \(P\left( A \right).P\left( B \right) = \frac{3}{5}.\frac{7}{8} = \frac{{21}}{{40}}\)
Vậy P(AB) = P(A).P(B).
Video hướng dẫn giải
Hai biến cố A và B trong HĐ1 độc lập hay không độc lập? Tại sao?
Phương pháp giải:
Cặp biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra của biển cố kia.
Lời giải chi tiết:
Nếu A xảy ra, tức là bạn Long lấy được quả bóng màu trắng từ hộp I. Vì bạn Hải lấy bóng từ hộp II vậy \(P\left( B \right) = \frac{7}{8}\)
Nếu A không xảy ra, tức là bạn Long lấy được quả bóng màu đen từ hộp I. Vì ban Hải lấy bóng từ hộp II vậy \(P\left( B \right) = \frac{7}{8}\)
Như vậy, xác suất xảy ra của biến cố B không thay đổi bởi việc xảy ra hay không xảy ra của biến cố A.
Vì hai bạn lấy từ 2 hộp khác nhau nên \(P\left( A \right) = \frac{3}{5}\) dù biến cố B xảy ra hay không xảy ra
Vậy A và B độc lập.
Video hướng dẫn giải
Các học sinh lớp 11D làm thí nghiệm gieo hai loại hạt giống A và B. Xác suất để hai loại hạt giống A và B nảy mầm tương ứng là 0,92 và 0,88. Giả sử việc nảy mầm của hạt A và hạt B là độc lập với nhau. Dùng sơ đồ hình cây, tính xác suất để:
a) Hạt giống A nảy mầm còn hạt giống B không nảy mầm;
b) Hạt giống A không nảy mầm còn hạt giống B nảy mầm;
c) Ít nhất có một trong hai loại hạt giống nảy mầm.
Phương pháp giải:
Nếu hai biến cố A và B độc lập với nhau thì P(AB) = P(A).P(B).
Lời giải chi tiết:
Ta dùng sơ đồ hình cây để mô tả như sau:
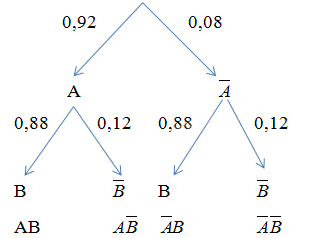
Theo sơ đồ hình cây, ta có:
a) \(P\left( {A\overline B } \right) = 0,92.0,12 = 0,1104\)
b) \(P\left( {\overline A B} \right) = 0,08.0,88 = 0,0704\)
c) \(P\left( {\overline A \overline B } \right) = 0,08.0,12 = 0,0096\)
\(P\left( {A \cup B} \right) = 1 - P\left( {\overline A \overline B } \right) = 1 - 0,0096 = 0,9904\)
Mục 1 của chương trình Toán 11 tập 2 Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa kiến thức về đạo hàm. Các bài tập trang 76 và 77 SGK Toán 11 tập 2 yêu cầu học sinh vận dụng các công thức, quy tắc đạo hàm đã học để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng tính toán là yếu tố then chốt để hoàn thành tốt các bài tập này.
Bài tập này yêu cầu học sinh tính đạo hàm của các hàm số đơn thức, đa thức, và các hàm số có dạng tổng, hiệu, tích, thương. Để giải bài tập này, học sinh cần áp dụng các quy tắc đạo hàm cơ bản như quy tắc đạo hàm của tổng, hiệu, tích, thương, và quy tắc đạo hàm của hàm hợp.
Bài tập này yêu cầu học sinh tìm đạo hàm của hàm số tại một điểm cụ thể. Để giải bài tập này, học sinh cần tính đạo hàm f'(x) và sau đó thay x = x0 vào f'(x) để tìm đạo hàm tại điểm x0.
Bài tập này yêu cầu học sinh tính đạo hàm cấp hai của hàm số, tức là đạo hàm của đạo hàm cấp một. Để giải bài tập này, học sinh cần tính đạo hàm cấp một f'(x) trước, sau đó tính đạo hàm của f'(x) để tìm đạo hàm cấp hai f''(x).
Ví dụ 1: Tính đạo hàm của hàm số y = 3x2 + 2x - 1.
Giải:
y' = (3x2)' + (2x)' - (1)' = 6x + 2 - 0 = 6x + 2.
Ví dụ 2: Tìm đạo hàm của hàm số y = sin(x) tại x = π/2.
Giải:
y' = cos(x). Thay x = π/2 vào y', ta được y' = cos(π/2) = 0.
Để củng cố kiến thức và kỹ năng giải bài tập đạo hàm, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 11 tập 2 và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tìm kiếm các bài giảng online về đạo hàm để hiểu rõ hơn về lý thuyết và phương pháp giải bài tập.
Việc giải bài tập mục 1 trang 76, 77 SGK Toán 11 tập 2 - Kết nối tri thức đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm và rèn luyện kỹ năng giải toán thường xuyên. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải quyết các bài tập này và đạt kết quả tốt trong môn Toán.