Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 1 - Kết nối tri thức. Mục 2 trang 85 là một phần quan trọng trong chương trình học, đòi hỏi học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, giúp bạn hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
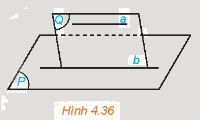
Cho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng b nằm trong (P). Gọi (Q) là mặt phẳng chứa a và b (H.4.36) Nếu a và (P) cắt nhau tại điểm M thì M có thuộc (Q) và M có thuộc b hay không? Hãy rút ra kết luận sau khi trả lời các câu hỏi trên.
Video hướng dẫn giải
Cho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng b nằm trong (P). Gọi (Q) là mặt phẳng chứa a và b (H.4.36).
Nếu a và (P) cắt nhau tại điểm M thì M có thuộc (Q) và M có thuộc b hay không? Hãy rút ra kết luận sau khi trả lời các câu hỏi trên.
Phương pháp giải:
Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P).
Lời giải chi tiết:
a thuộc (Q) suy ra nếu a cắt (P) thì M thuộc giao tuyến của (Q) và (P) hay a thuộc b.
Tuy nhiên a // b suy ra không thể xảy ra trường hợp a cắt (P).
Kết luận: Nếu a không nằm trong (P) và song song với b thuộc (P) thì a song song với (P) hay a và (P) không có điểm chung.
Video hướng dẫn giải
Trong Ví dụ 2, chứng minh rằng đường thẳng c song song với mp(a,b), đường thẳng b song song với mp(a,c).
Phương pháp giải:
Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P).
Lời giải chi tiết:
Ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng nên đường thẳng c không nằm trong mp (a, b). Vì đường thẳng c song song song với đường thẳng b và đường thẳng b nằm trong mp (a, b) nên đường thẳng c song song với mp (a, b).
Ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng nên đường thẳng a không nằm trong mp (a, c). Vì đường thẳng b song song song với đường thẳng c và đường thẳng c nằm trong mp (a, c) nên đường thẳng b song song với mp (a, c).
Video hướng dẫn giải
Cho hình chóp S.ABCD có đáy là hình thang (AB//CD). Hai đường thẳng SD và AB có chéo nhau hay không? Chỉ ra mặt phẳng chứa đường thẳng SD và song song với AB.
Phương pháp giải:
Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P).
Lời giải chi tiết:
Ta có: SD và AB chéo nhau.
Vì AB và SD chéo nhau nên AB không nằm trong mp(SCD).
Vì AB // CD nên AB // mp(SCD).
Vậy (SCD) là mặt phẳng chứa SD và song song với AB.
Video hướng dẫn giải
Trong tình huống mở đầu, hãy giải thích tại sao dây nhợ khi căng thì song song với mặt đất. Tác dụng của việc đó là gì?
Phương pháp giải:
Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P).
Lời giải chi tiết:
Khi dây nhợ căng ra sẽ tạo thành một đường thẳng. Vì dây không chạm đất nên dây song song với mặt đất.
Tác dụng: Nhờ có dây nhợ được căng ra, bức tường xây được sẽ tạo thành một mặt phẳng vuông góc với mặt đất.
Video hướng dẫn giải
Cho đường thẳng a song song với mặt phẳng (P) và (Q) là một mặt phẳng chứa a. Giả sử (Q) cắt (P) theo giao tuyến b (H. 4.36)
a) Hai đường thẳng a và b có thể chéo nhau không?
b) Hai đường thẳng a và b có thể cắt nhau không?
Phương pháp giải:
- Hai đường thẳng cắt nhau là hai đường thẳng nằm trong cùng 1 mặt phẳng có ít nhất 1 điểm chung.
- Hai đường thẳng chéo là hai đường thẳng cùng không nằm trong 1 mặt phẳng.
Lời giải chi tiết:
a) (Q) cắt (P) theo giao tuyến b suy ra b thuộc (Q).
Do đó a và b không thể chéo nhau.
b) Vì a // (P) và b thuộc (P) suy ra a và b không thể cắt nhau.
Video hướng dẫn giải
Trong Ví dụ 4, gọi (Q) là mặt phẳng qua E và song song với hai đường thẳng AB, AD. Xác định giao tuyến của (Q) với các mặt của tứ diện.
Phương pháp giải:
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b song song với a.
Lời giải chi tiết:
Mặt phẳng (ABC) chứa đường thẳng AB song song với (Q) nên mp(ABC) cắt mp(Q) theo giao tuyến song song với AB. Vẽ EF // AB (F thuộc BC) thì EF là giao tuyến của (Q) và (ABC).
Hai mặt phẳng (ACD) và (ABD) cùng chứa đường thẳng AD song song với (Q) nên chúng cắt mặt phẳng (Q) theo giao tuyến song song với với AD. Vẽ EK song song với AD (K thuộc CD) thì EK, FK lần lượt là giao tuyến của mp(Q) với hai mp(ACD) và (BCD).
Mục 2 trang 85 SGK Toán 11 tập 1 - Kết nối tri thức thường tập trung vào các bài toán liên quan đến phép biến hình, đặc biệt là phép tịnh tiến, phép quay, và phép đối xứng. Việc nắm vững các tính chất của các phép biến hình này là nền tảng để giải quyết các bài toán hình học phức tạp hơn trong chương trình học.
Mục 2 thường bao gồm các dạng bài tập sau:
Để giải tốt các bài tập trong Mục 2 trang 85, học sinh cần:
Bài tập: Cho điểm A(1; 2) và phép tịnh tiến theo vectơ v = (3; -1). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến đó.
Giải:
Áp dụng công thức phép tịnh tiến:
A'(x' ; y') = A(x; y) + v(a; b) = (x + a; y + b)
Thay số vào, ta có:
A'(1 + 3; 2 - 1) = A'(4; 1)
Vậy, tọa độ điểm A' là (4; 1).
Để củng cố kiến thức và kỹ năng giải bài tập trong Mục 2 trang 85, học sinh nên:
Các kiến thức về phép biến hình có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học kỹ thuật, như hình học giải tích, đồ họa máy tính, và vật lý. Việc nắm vững kiến thức này sẽ giúp học sinh có nền tảng vững chắc để học tập và nghiên cứu các lĩnh vực khác.
Hy vọng với những hướng dẫn chi tiết trên, bạn sẽ tự tin giải quyết các bài tập trong Mục 2 trang 85 SGK Toán 11 tập 1 - Kết nối tri thức. Chúc bạn học tập tốt!