Bài học này cung cấp kiến thức nền tảng về các số đặc trưng đo xu thế trung tâm của một tập dữ liệu, bao gồm trung bình cộng, trung vị và mốt. Đây là những khái niệm quan trọng trong thống kê, giúp chúng ta hiểu rõ hơn về sự phân bố và đặc điểm của dữ liệu.
Chúng tôi sẽ trình bày lý thuyết một cách dễ hiểu, kèm theo các ví dụ minh họa cụ thể để bạn có thể nắm bắt kiến thức một cách nhanh chóng và hiệu quả. Học cùng giaitoan.edu.vn để chinh phục môn Toán 11!
1. Số trung bình của mẫu số liệu ghép nhóm
1. Số trung bình của mẫu số liệu ghép nhóm
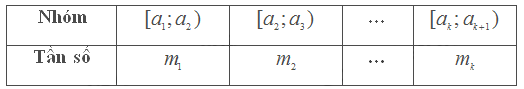
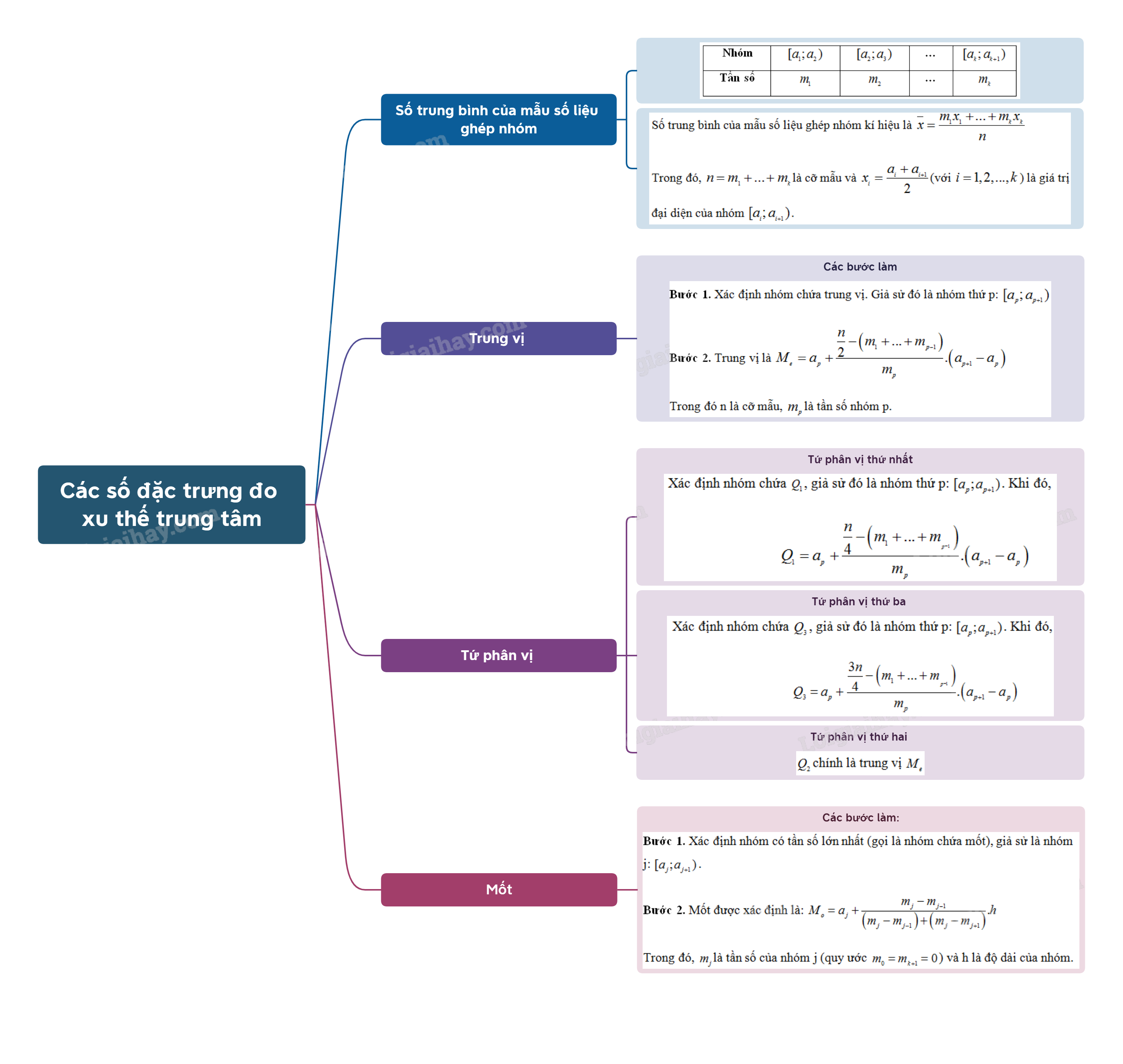
Số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\)
Trong đó, \(n = {m_1} + ... + {m_k}\) là cỡ mẫu và \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\)(với \(i = 1,2,...,k\)) là giá trị đại diện của nhóm \({\rm{[}}{a_i};{a_{i + 1}})\).
2. Trung vị của mẫu số liệu ghép nhóm
Để tính trung vị của mẫu số liệu ghép nhóm, ta làm như sau:
Bước 1. Xác định nhóm chứa trung vị. Giả sử đó là nhóm thứ p: \({\rm{[}}{a_p};{a_{p + 1}})\).
Bước 2. Trung vị là \({M_e} = {a_p} + \frac{{\frac{n}{2} - \left( {{m_1} + ... + {m_{p - 1}}} \right)}}{{{m_p}}}.\left( {{a_{p + 1}} - {a_p}} \right)\)
Trong đó n là cỡ mẫu, \({m_p}\) là tần số nhóm p.
Với \(p = 1\), ta quy ước \({m_1} + ... + {m_{p - 1}} = 0\)
3. Tứ phân vị của mấu số liệu ghép nhóm
Để tính tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_1}\), giả sử đó là nhóm thứ p: \({\rm{[}}{a_p};{a_{p + 1}})\). Khi đó,
\({Q_1} = {a_p} + \frac{{\frac{n}{4} - \left( {{m_1} + ... + {m_{_{p - 1}}}} \right)}}{{{m_p}}}.\left( {{a_{p + 1}} - {a_p}} \right)\)
Trong đó n là cỡ mẫu, \({m_p}\) là tần số nhóm p.
Với \(p = 1\), ta quy ước \({m_1} + ... + {m_{p - 1}} = 0\)
Để tính tứ phân vị thứ ba \({Q_3}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_3}\), giả sử đó là nhóm thứ p: \({\rm{[}}{a_p};{a_{p + 1}})\). Khi đó,
\({Q_3} = {a_p} + \frac{{\frac{{3n}}{4} - \left( {{m_1} + ... + {m_{_{p - 1}}}} \right)}}{{{m_p}}}.\left( {{a_{p + 1}} - {a_p}} \right)\)
Trong đó n là cỡ mẫu, \({m_p}\) là tần số nhóm p. Với \(p = 1\), ta quy ước \({m_1} + ... + {m_{p - 1}} = 0\)
Tứ phân vị thứ hai \({Q_2}\) chính là trung vị \({M_e}\).
4. Mốt của mẫu số liệu ghép nhóm
Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:
Bước 1. Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm j: \({\rm{[}}{a_j};{a_{j + 1}})\).
Bước 2. Mốt được xác định là: \({M_o} = {a_j} + \frac{{{m_j} - {m_{j - 1}}}}{{\left( {{m_j} - {m_{j - 1}}} \right) + \left( {{m_j} - {m_{j + 1}}} \right)}}.h\)
Trong đó, \({m_j}\) là tần số của nhóm j (quy ước \({m_0} = {m_{k + 1}} = 0\)) và h là độ dài của nhóm.
Người ta chỉ định nghĩa mốt cho mẫu ghép nhóm có độ dài các nhóm bằng nhau. Một mẫu có thể không có mốt hoặc có nhiều hơn một mốt.
Mốt của mẫu số liệu ghép nhóm xấp xỉ cho mốt của mẫu số liệu gốc, nó được dùng để đo xu thế trung tâm của mẫu số liệu.
Trong thống kê, các số đặc trưng đo xu thế trung tâm đóng vai trò quan trọng trong việc tóm tắt và mô tả một tập dữ liệu. Chúng cung cấp thông tin về giá trị điển hình hoặc trung tâm của dữ liệu, giúp chúng ta hiểu rõ hơn về sự phân bố và đặc điểm của nó. Bài viết này sẽ trình bày chi tiết về các số đặc trưng đo xu thế trung tâm trong chương trình Toán 11 Kết nối tri thức, bao gồm trung bình cộng, trung vị và mốt.
Trung bình cộng (mean) là tổng của tất cả các giá trị trong một tập dữ liệu chia cho số lượng giá trị đó. Công thức tính trung bình cộng:
x̄ = (∑xi) / n
Trong đó:
x̄ là trung bình cộng∑xi là tổng của tất cả các giá trị trong tập dữ liệun là số lượng giá trị trong tập dữ liệuVí dụ: Cho tập dữ liệu 2, 4, 6, 8, 10. Trung bình cộng của tập dữ liệu này là (2 + 4 + 6 + 8 + 10) / 5 = 6.
Trung vị (median) là giá trị nằm ở giữa một tập dữ liệu đã được sắp xếp theo thứ tự tăng dần hoặc giảm dần. Nếu số lượng giá trị trong tập dữ liệu là lẻ, trung vị là giá trị ở giữa. Nếu số lượng giá trị là chẵn, trung vị là trung bình cộng của hai giá trị ở giữa.
Ví dụ 1: Cho tập dữ liệu 2, 4, 6, 8, 10. Trung vị của tập dữ liệu này là 6.
Ví dụ 2: Cho tập dữ liệu 2, 4, 6, 8. Trung vị của tập dữ liệu này là (4 + 6) / 2 = 5.
Mốt (mode) là giá trị xuất hiện nhiều nhất trong một tập dữ liệu. Một tập dữ liệu có thể có một mốt (unimodal), nhiều mốt (multimodal) hoặc không có mốt nào (nếu tất cả các giá trị đều xuất hiện với tần số bằng nhau).
Ví dụ: Cho tập dữ liệu 2, 4, 4, 6, 8. Mốt của tập dữ liệu này là 4.
Mối quan hệ giữa trung bình cộng, trung vị và mốt có thể cung cấp thông tin về sự phân bố của dữ liệu:
Các số đặc trưng đo xu thế trung tâm được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
Hãy tự giải các bài tập sau để củng cố kiến thức:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết các số đặc trưng đo xu thế trung tâm. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào thực tế.