Chào mừng bạn đến với bài học về lý thuyết Công thức cộng xác suất trong chương trình Toán 11 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về công thức cộng xác suất, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, điều kiện áp dụng, các ví dụ minh họa và bài tập thực hành để bạn có thể nắm vững kiến thức này.
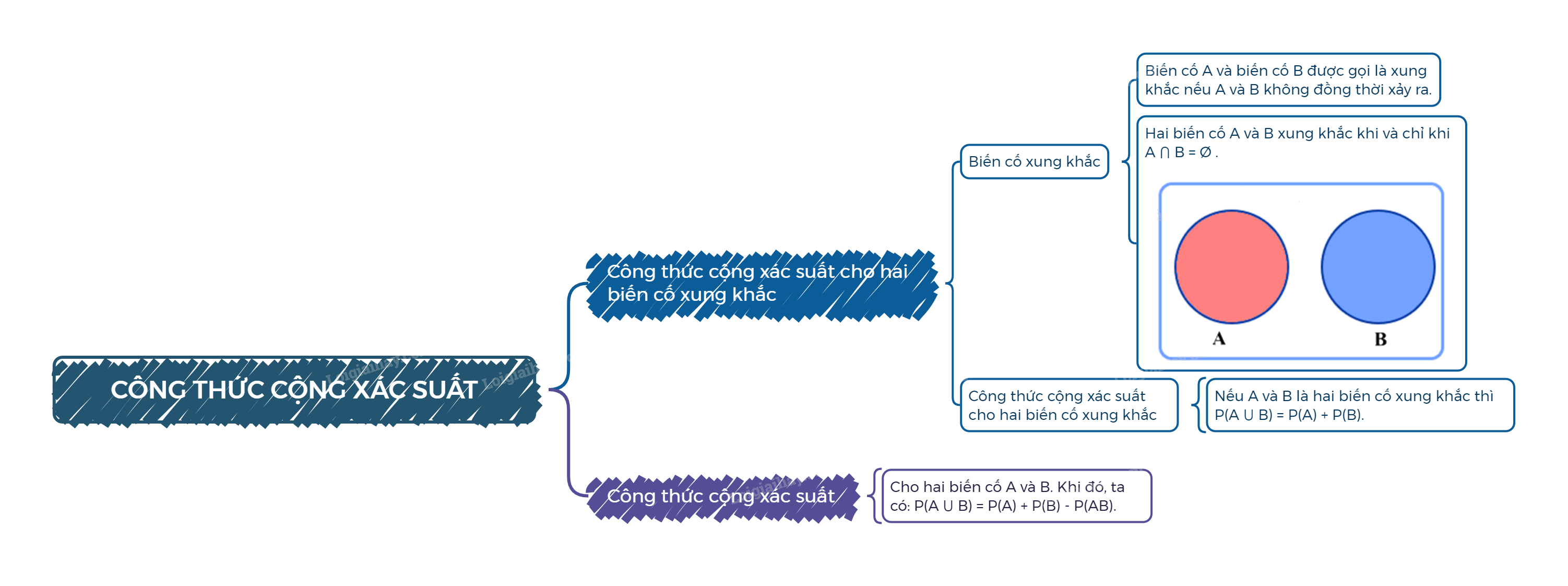
1. Công thức cộng xác suất cho hai biến cố xung khắc a) Biến cố xung khắc
1. Công thức cộng xác suất cho hai biến cố xung khắc
a) Biến cố xung khắc
Biến cố A và biến cố B được gọi là xung khắc nếu A và B không đồng thời xảy ra.
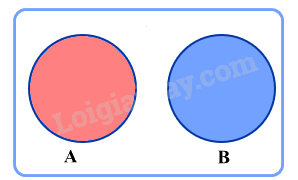
b) Công thức cộng xác suất cho hai biến cố xung khắc
Nếu A và B là hai biến cố xung khắc thì \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).
2. Công thức cộng xác suất
Cho hai biến cố A và B. Khi đó, ta có:
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right)\).
Công thức này được gọi là công thức cộng xác suất.
Trong chương trình Toán 11 Kết nối tri thức, phần xác suất đóng vai trò quan trọng trong việc rèn luyện tư duy logic và khả năng giải quyết vấn đề. Một trong những công cụ cơ bản và hữu ích nhất trong phần này là công thức cộng xác suất. Bài viết này sẽ đi sâu vào lý thuyết, điều kiện áp dụng, các ví dụ minh họa và bài tập thực hành để giúp bạn nắm vững kiến thức này.
Trước khi đi vào công thức cộng xác suất, chúng ta cần ôn lại khái niệm về xác suất. Xác suất của một sự kiện A, ký hiệu là P(A), là một số thực nằm trong khoảng [0, 1], biểu thị khả năng xảy ra của sự kiện đó. P(A) = 0 nghĩa là sự kiện A không thể xảy ra, P(A) = 1 nghĩa là sự kiện A chắc chắn xảy ra.
Để hiểu rõ công thức cộng xác suất, chúng ta cần phân biệt các loại sự kiện:
Công thức cộng xác suất được sử dụng để tính xác suất của một trong hai sự kiện A hoặc B xảy ra. Công thức này có hai dạng, tùy thuộc vào việc hai sự kiện A và B có xung khắc hay không:
Nếu A và B là hai sự kiện xung khắc, thì xác suất của A hoặc B xảy ra được tính bằng:
P(A ∪ B) = P(A) + P(B)
Trong đó:
Nếu A và B là hai sự kiện không xung khắc, thì xác suất của A hoặc B xảy ra được tính bằng:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
Trong đó:
Ví dụ 1: Một hộp chứa 5 quả bóng đỏ và 3 quả bóng xanh. Lấy ngẫu nhiên 1 quả bóng từ hộp. Tính xác suất để quả bóng được lấy ra là màu đỏ hoặc màu xanh.
Giải:
Ví dụ 2: Gieo một con xúc xắc 6 mặt. Tính xác suất để mặt xuất hiện là số chẵn hoặc số chia hết cho 3.
Giải:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về lý thuyết công thức cộng xác suất trong chương trình Toán 11 Kết nối tri thức. Chúc bạn học tập tốt!