Chào mừng bạn đến với bài học lý thuyết về phương trình, bất phương trình mũ và lôgarit trong chương trình Toán 11 Kết nối tri thức. Đây là một phần kiến thức quan trọng, nền tảng cho các bài toán nâng cao và các môn học liên quan sau này.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, dễ hiểu, giúp bạn nắm vững các khái niệm, định lý và phương pháp giải bài tập liên quan đến chủ đề này.
1. Phương trình mũ
1. Phương trình mũ
Phương trình mũ cơ bản có dạng \({a^x} = b\)(với \(0 < a \ne 1\)).
- Nếu b > 0 thì phương trình có nghiệm duy nhất \(x = {\log _a}b\).
- Nếu b \( \le \) 0 thì phương trình vô nghiệm.
Minh họa bằng đồ thị:
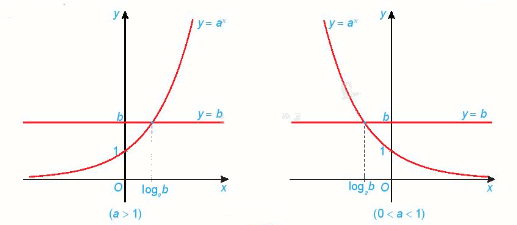
Chú ý: Phương pháp giải phương trình mũ bằng cách đưa về cùng cơ số:
Nếu \(0 < a \ne 1\) thì \({a^u} = {a^v} \Leftrightarrow u = v\).
2. Phương trình lôgarit
Phương trình lôgarit cơ bản có dạng \({\log _a}x = b\left( {0 < a \ne 1} \right)\).
Phương trình lôgarit cơ bản \({\log _a}x = b\) có nghiệm duy nhất \(x = {a^b}\).
Minh họa bằng đồ thị:
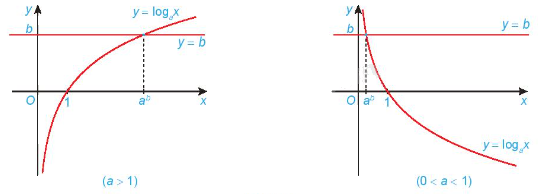
Chú ý: Phương pháp giải phương trình lôgarit bằng cách đưa về cùng cơ số:
Nếu \(u,v > 0\) và \(0 < a \ne 1\) thì \({\log _a}u = {\log _a}v \Leftrightarrow u = v\).
3. Bất phương trình mũ
Bất phương trình mũ cơ bản có dạng \({a^x} > b\) (hoặc \({a^x} \ge b,{a^x} < b,{a^x} \le b\)) với \(a > 0,a \ne 1\).
Xét bất phương trình dạng \({a^x} > b\):
- Nếu \(b \le 0\) thì tập nghiệm của bất phương trình là \(\mathbb{R}\).
- Nếu b > 0 thì bất phương trình tương đương với \({a^x} > {a^{{{\log }_a}b}}\).
Với a > 1, nghiệm của bất phương trình là \(x > {\log _a}b\).
Với \(0 < a < 1\), nghiệm của bất phương trình là \(x < {\log _a}b\).
Chú ý:
a) Các bất phương trình mũ cơ bản còn lại được giải tương tự.
b) Nếu a > 1 thì \({a^u} > {a^v} \Leftrightarrow u > v\).
Nếu 0 < a < 1 thì \({a^u} > {a^v} \Leftrightarrow u < v\).
4. Bất phương trình lôgarit
Bất phương trình lôgarit cơ bản có dạng \({\log _a}x > b\)(hoặc \({\log _a}x \ge b,{\log _a}x < b,{\log _a}x \le b\)) với \(a > 0,a \ne 1\).
Xét bất phương trình dạng \({\log _a}x > b\):
- Nếu a > 1 thì nghiệm của bất phương trình là \(x > {a^b}\).
- Nếu 0 < a < 1 thì nghiệm của bất phương trình là \(0 < x < {a^b}\).
Chú ý:
a) Các bất phương trình lôgarit cơ bản còn lại được giải tương tự.
b) Nếu a > 1 thì \({\log _a}u > {\log _a}v \Leftrightarrow u > v > 0\).
Nếu 0 < a < 1 thì \({\log _a}u > {\log _a}v \Leftrightarrow 0 < u < v\).
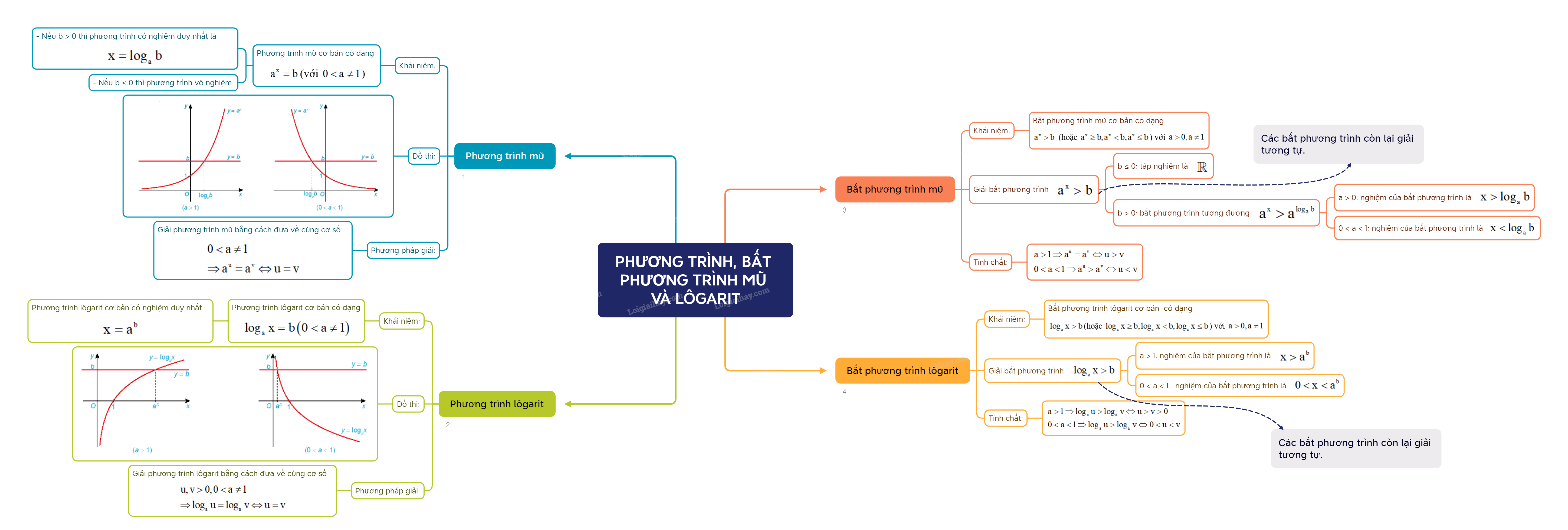
Chương trình Toán 11 Kết nối tri thức, phần Phương trình, bất phương trình mũ và lôgarit đóng vai trò then chốt trong việc xây dựng nền tảng vững chắc cho các kiến thức toán học nâng cao. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết, các dạng bài tập thường gặp và phương pháp giải quyết chúng.
1. Phương trình mũ: Là phương trình có chứa ẩn số trong số mũ. Dạng tổng quát: ax = b (với a > 0, a ≠ 1).
2. Bất phương trình mũ: Là bất phương trình có chứa ẩn số trong số mũ. Dạng tổng quát: ax > b (với a > 0, a ≠ 1).
3. Lôgarit: Lôgarit cơ số a của b (ký hiệu logab) là số x sao cho ax = b. Điều kiện: a > 0, a ≠ 1, b > 0.
4. Phương trình lôgarit: Là phương trình có chứa ẩn số trong biểu thức lôgarit. Dạng tổng quát: logaf(x) = b.
5. Bất phương trình lôgarit: Là bất phương trình có chứa ẩn số trong biểu thức lôgarit. Dạng tổng quát: logaf(x) > b.
Tương tự như phương trình mũ, ta có thể sử dụng các phương pháp sau:
Tương tự như phương trình lôgarit, cần chú ý đến điều kiện và sử dụng các tính chất của lôgarit một cách cẩn thận. Khi cơ số lớn hơn 1, bất phương trình giữ nguyên chiều. Khi cơ số nhỏ hơn 1, bất phương trình đổi chiều.
Ví dụ 1: Giải phương trình 2x = 8
Ta có 8 = 23, suy ra 2x = 23. Vậy x = 3.
Ví dụ 2: Giải bất phương trình log2(x + 1) > 3
Điều kiện: x + 1 > 0, hay x > -1.
Ta có x + 1 > 23 = 8, suy ra x > 7.
Kết hợp điều kiện, ta có nghiệm x > 7.
Để nắm vững kiến thức về phương trình, bất phương trình mũ và lôgarit, bạn nên luyện tập thường xuyên với các bài tập khác nhau. Hãy tìm kiếm các tài liệu tham khảo, bài giảng online và các bài tập trắc nghiệm để củng cố kiến thức của mình.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết Phương trình, bất phương trình mũ và lôgarit - Toán 11 Kết nối tri thức. Chúc bạn học tập tốt!