Bài 7.5 trang 36 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Kết nối tri thức. Bài học này tập trung vào việc giải quyết các bài toán liên quan đến đạo hàm của hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Cho hình chóp S.ABC có đáy là tam giác cân tại A và SA ( bot ) (ABC). Gọi M là trung điểm của BC. Chứng minh rằng:
Đề bài
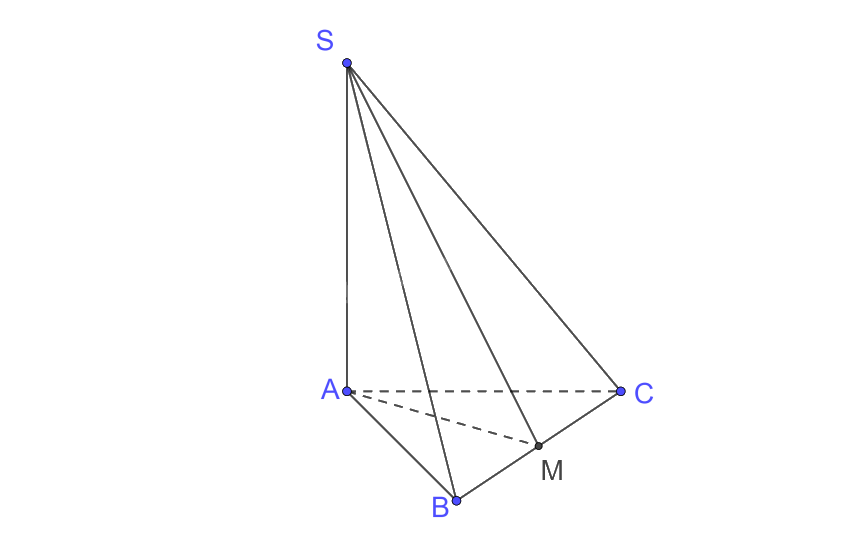
Cho hình chóp S.ABC có đáy là tam giác cân tại A và SA \( \bot \) (ABC). Gọi M là trung điểm của BC. Chứng minh rằng:
a) BC \( \bot \) (SAM);
b) Tam giác SBC cân tại S.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.
Lời giải chi tiết
a) Xét tam giác ABC cân tại A có
AM là đường trung tuyến (M là trung điểm BC)
\( \Rightarrow \) AM là đường cao \( \Rightarrow \) \(AM \bot BC\)
Ta có:
\(\left. \begin{array}{l}AM \bot BC\\SA \bot BC\left( {SA \bot \left( {ABC} \right)} \right)\\AM \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAM} \right)\)
b) \(\left. \begin{array}{l}BC \bot \left( {SAM} \right)\\SM \subset \left( {SAM} \right)\end{array} \right\} \Rightarrow BC \bot SM\)
Xét tam giác SBC có:
+) SM là đường cao \(\left( {BC \bot SM} \right)\)
+) SM là đường trung tuyến (M là trung điểm BC)
\( \Rightarrow \) Tam giác SBC cân tại S.
Bài 7.5 trang 36 SGK Toán 11 tập 2 – Kết nối tri thức là một phần quan trọng trong chương trình học về đạo hàm của hàm số. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, quy tắc tính đạo hàm và các ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
Bài tập 7.5 bao gồm các câu hỏi và bài tập khác nhau, yêu cầu học sinh:
Để giúp học sinh giải quyết bài tập 7.5 một cách hiệu quả, chúng tôi cung cấp hướng dẫn giải chi tiết cho từng câu hỏi và bài tập. Hướng dẫn này bao gồm:
Ví dụ 1: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = 3x2 + 4x - 5
Ví dụ 2: Tìm đạo hàm của hàm số g(x) = sin(x) + cos(x) tại x = π/2.
Giải:
g'(x) = cos(x) - sin(x)
g'(π/2) = cos(π/2) - sin(π/2) = 0 - 1 = -1
Để đạt được kết quả tốt nhất khi giải bài tập 7.5, học sinh cần lưu ý:
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Để hiểu sâu hơn về đạo hàm và các ứng dụng của nó, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng hướng dẫn giải chi tiết bài tập 7.5 trang 36 SGK Toán 11 tập 2 – Kết nối tri thức này sẽ giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả. Chúc các em học tập tốt!