Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 23, 24, 25 sách giáo khoa Toán 11 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho hai hàm số \(f\left( x \right) = {x^2}\) và \(g\left( x \right) = {x^3}\), với các đồ thị như hình dưới đây.
Cho hai hàm số \(f\left( x \right) = {x^2}\) và \(g\left( x \right) = {x^3}\), với các đồ thị như hình dưới đây.
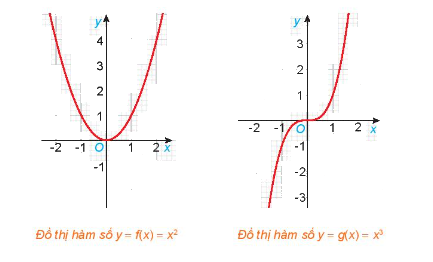
a) Tìm các tập xác định \({D_f},\;{D_g}\) của các hàm số \(f\left( x \right)\) và \(g\left( x \right)\).
b) Chứng tỏ rằng \(f\left( { - x} \right) = f\left( x \right),\;\forall x \in {D_f}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = f\left( x \right)\) đối với hệ trục tọa độ Oxy?
c) Chứng tỏ rằng \(g\left( { - x} \right) = - g\left( x \right),\;\forall x \in {D_g}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = g\left( x \right)\) đối với hệ trục tọa độ Oxy?
Phương pháp giải:
Hàm số \(f\left( x \right)\) và \(g\left( x \right)\) luôn xác định với mọi \(x \in \mathbb{R}\)
Lời giải chi tiết:
a) Tập xác định của hàm số đã cho là: \({D_f} = \mathbb{R};\;{D_g} = \mathbb{R}\)
b) Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2} = f\left( x \right)\)
Đồ thị của hàm số \(y = f\left( x \right) = {x^2}\) đối xứng qua trục tung
c) Ta có: \(g\left( { - x} \right) = {\left( { - x} \right)^3} = - {x^3} = - g\left( x \right)\)
Đồ thị của hàm số \(y = g\left( x \right) = {x^3}\) đối xứng qua gốc tọa độ
Xét tính chẵn, lẻ của hàm số \(g\left( x \right) = \frac{1}{x}\).
Phương pháp giải:
Sử dụng định nghĩa về hàm số chẵn, lẻ
Lời giải chi tiết:
Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ 0 \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(g\left( { - x} \right) = \frac{1}{{ - x}} = - \frac{1}{x} = - g\left( x \right),\;\forall x\; \in \;D\).
Vậy \(g\left( x \right) = \frac{1}{x}\) là hàm số lẻ
So sánh:
a) \(\sin \left( {x + 2\pi } \right)\) và \(\sin x\);
b) \(\cos (x + 2\pi )\) và \(\cos x\);
c) \(\tan \left( {x + \pi } \right)\) và \(\tan x\);
d) \(\cot (x + \pi )\) và \(\cot x\).
Lời giải chi tiết:
Ta có:
a) \(\sin \left( {x + 2\pi } \right) = \sin x\) với mọi \(x\; \in \;\mathbb{R}\)
b) \(\cos \left( {x + 2\pi } \right) = \cos x\) với mọi \(x\; \in \;\mathbb{R}\)
c) \(\tan \left( {x + \pi } \right) = \tan x\) với mọi \(x \ne \frac{\pi }{2} + k\pi ,\;k\; \in \;\mathbb{Z}\)
d) \(\cot \left( {x + \pi } \right) = \cot x\) với mọi \(x \ne \frac{\pi }{2} + k\pi ,\;k\; \in \;\mathbb{Z}\)
Xét tính tuần hoàn của hàm số \(y = \tan 2x\).
Phương pháp giải:
Hàm số \(y = \tan \left( {ax + b} \right)\) tuần hoàn với chu kỳ \(T = \frac{\pi }{{\left| a \right|}}\)
Lời giải chi tiết:
Hàm số có tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,\;k\; \in \;\mathbb{Z}} \right\}\) và với mọi số thực x, ta có:
\(\left( {x - \frac{\pi }{2}} \right) \in \;\mathbb{R},\;\left( {x + \frac{\pi }{2}} \right) \in \;\mathbb{R},\)
\(\tan 2\left( {x + \frac{\pi }{2}} \right) = \tan \left( {2x + \pi } \right) = \tan 2x\)
Vậy \(y = \tan 2x\;\)là hàm số tuần hoàn
Mục 2 của chương trình Toán 11 tập 1 - Kết nối tri thức tập trung vào các kiến thức cơ bản về hàm số bậc hai. Các bài tập trang 23, 24, 25 SGK Toán 11 tập 1 yêu cầu học sinh vận dụng các kiến thức về định nghĩa, tính chất, đồ thị và ứng dụng của hàm số bậc hai để giải quyết các bài toán cụ thể.
Bài tập này yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai được cho dưới dạng tổng quát y = ax2 + bx + c. Để làm được bài này, học sinh cần nắm vững định nghĩa của hàm số bậc hai và biết cách nhận biết các hệ số a, b, c.
Ví dụ: Cho hàm số y = 2x2 - 5x + 1. Hệ số a = 2, b = -5, c = 1.
Tập xác định của hàm số là tập hợp tất cả các giá trị của x mà tại đó hàm số có nghĩa. Đối với hàm số bậc hai, tập xác định là tập R (tập hợp tất cả các số thực) trừ khi mẫu số bằng 0 (nếu hàm số là phân thức).
Ví dụ: Hàm số y = x2 + 1 có tập xác định là R.
Để vẽ đồ thị của hàm số bậc hai, học sinh cần xác định các yếu tố quan trọng như đỉnh, trục đối xứng, giao điểm với trục hoành và trục tung. Sau đó, vẽ các điểm và nối chúng lại để tạo thành đồ thị parabol.
Các bước vẽ đồ thị:
Nếu a > 0, hàm số có giá trị nhỏ nhất tại đỉnh I(x0, y0). Giá trị nhỏ nhất là y0.
Nếu a < 0, hàm số có giá trị lớn nhất tại đỉnh I(x0, y0). Giá trị lớn nhất là y0.
Hàm số bậc hai có nhiều ứng dụng trong thực tế, chẳng hạn như:
Khi giải bài tập về hàm số bậc hai, học sinh cần:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh đã có thể tự tin giải các bài tập mục 2 trang 23, 24, 25 SGK Toán 11 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!
| Bài tập | Nội dung chính |
|---|---|
| Bài 1 | Xác định hệ số a, b, c |
| Bài 2 | Tìm tập xác định |
| Bài 3 | Vẽ đồ thị |
| Bài 4 | Tìm giá trị lớn nhất, nhỏ nhất |