Chào mừng bạn đến với bài học về lý thuyết biến cố hợp, biến cố giao và biến cố độc lập trong chương trình Toán 11 Kết nối tri thức. Đây là một phần kiến thức quan trọng trong chương xác suất, giúp bạn hiểu rõ hơn về các khái niệm cơ bản và ứng dụng của chúng trong thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập vận dụng đa dạng để giúp bạn nắm vững kiến thức một cách hiệu quả nhất.
1. Biến cố hợp
1. Biến cố hợp
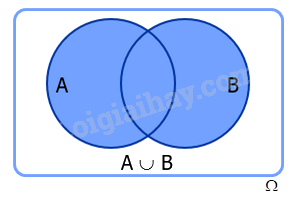
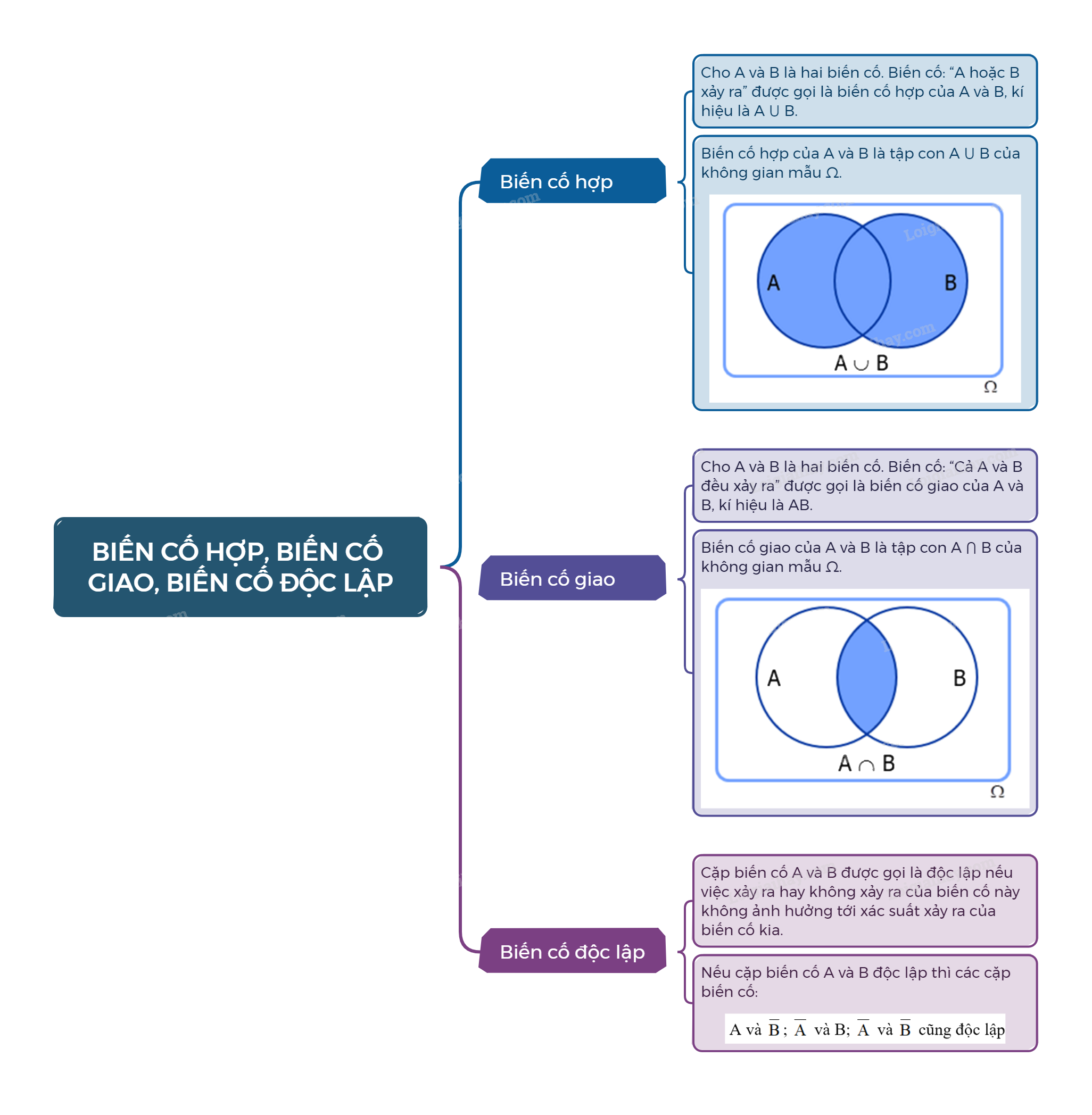
Cho A và B là hai biến cố. Biến cố: “A hoặc B xảy ra” được gọi là biến cố hợp của A và B, kí hiệu là \(A \cup B\).
Biến cố hợp của A và B là tập con \(A \cup B\) của không gian mẫu \(\Omega \).
2. Biến cố giao
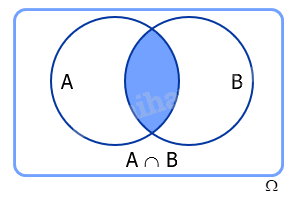
Cho A và B là hai biến cố. Biến cố: “Cả A và B đều xảy ra” được gọi là biến cố giao của A và B, kí hiệu là AB.
Biến cố giao của A và B là tập con \(A \cap B\) của không gian mẫu \(\Omega \).
3. Biến cố độc lập
Cặp biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra của biến cố kia.
Chú ý: Nếu cặp biến cố A và B độc lập thì các cặp biến cố: A và \(\overline B \); \(\overline A \) và B; \(\overline A \) và \(\overline B \) cũng độc lập.
Trong chương trình Toán 11 Kết nối tri thức, phần xác suất đóng vai trò quan trọng trong việc trang bị cho học sinh những kiến thức cơ bản về lý thuyết xác suất và ứng dụng của nó. Một trong những nội dung cốt lõi của chương này là lý thuyết về biến cố hợp, biến cố giao và biến cố độc lập. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về các khái niệm này, cùng với các ví dụ minh họa để giúp bạn hiểu rõ hơn.
Trước khi đi sâu vào các loại biến cố, chúng ta cần hiểu rõ khái niệm biến cố. Một biến cố là một sự kiện có thể xảy ra hoặc không xảy ra trong một phép thử nào đó. Ví dụ, khi tung một đồng xu, biến cố 'mặt ngửa xuất hiện' là một biến cố.
Biến cố hợp của hai biến cố A và B (ký hiệu là A ∪ B) là biến cố xảy ra khi ít nhất một trong hai biến cố A hoặc B xảy ra. Nói cách khác, A ∪ B xảy ra nếu A xảy ra, B xảy ra, hoặc cả A và B đều xảy ra.
Ví dụ: Khi tung một xúc xắc, xét biến cố A: 'xuất hiện mặt số chẵn' và biến cố B: 'xuất hiện mặt số lớn hơn 3'. Khi đó, A ∪ B là biến cố 'xuất hiện mặt số chẵn hoặc mặt số lớn hơn 3'. Các kết quả thỏa mãn A ∪ B là {2, 4, 6, 4, 5, 6}.
Biến cố giao của hai biến cố A và B (ký hiệu là A ∩ B) là biến cố xảy ra khi cả hai biến cố A và B đều xảy ra. Nói cách khác, A ∩ B chỉ xảy ra khi cả A và B đồng thời xảy ra.
Ví dụ: Tiếp tục ví dụ trên, A ∩ B là biến cố 'xuất hiện mặt số chẵn và mặt số lớn hơn 3'. Các kết quả thỏa mãn A ∩ B là {4, 6}.
Hai biến cố A và B được gọi là độc lập nếu việc xảy ra của biến cố A không ảnh hưởng đến xác suất xảy ra của biến cố B, và ngược lại. Công thức kiểm tra tính độc lập của hai biến cố là: P(A ∩ B) = P(A) * P(B).
Ví dụ: Khi tung hai đồng xu độc lập, biến cố A: 'đồng xu thứ nhất xuất hiện mặt ngửa' và biến cố B: 'đồng xu thứ hai xuất hiện mặt sấp' là hai biến cố độc lập. Xác suất để cả hai đồng xu đều xuất hiện mặt ngửa là (1/2) * (1/2) = 1/4.
Bài 1: Một hộp chứa 5 quả bóng đỏ và 3 quả bóng xanh. Lấy ngẫu nhiên 2 quả bóng từ hộp. Tính xác suất để lấy được 1 quả bóng đỏ và 1 quả bóng xanh.
Bài 2: Tung hai con xúc xắc. Tính xác suất để tổng số chấm trên hai con xúc xắc bằng 7.
Lý thuyết biến cố có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Hi vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết biến cố hợp, biến cố giao và biến cố độc lập trong chương trình Toán 11 Kết nối tri thức. Hãy luyện tập thêm các bài tập để nắm vững kiến thức và áp dụng chúng vào giải quyết các bài toán thực tế.