Bài 4.21 trang 93 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Cầu thang xương cá là dạng cầu thang có hình dáng tương tư như những đốt xương cá, thường có những bậc thang với khoảng mở lớn, tạo được sự nhẹ nhàng và thoáng đãng cho không gian sông. Trong Hình 4.55, phần mép của mỗi bậc thang, nằm trên tường song song với nhau. Hãy giải thích tại sao.
Đề bài
Trong không gian cho ba mặt phẳng phân biệt (P), (Q), (R). Những mệnh đề nào sau đây là đúng?
a) Nếu (P) chứa một đường thẳng song song với (Q) thì (P) song song với (Q).
b) Nếu (P) chứa hai đường thẳng song song với (Q) thì (P) song song với (Q).
c) Nếu (P) và (Q) song song với (R) thì (P) song song với (Q).
d) Nếu (P) và (Q) cắt (R) thì (P) và (Q) song song với nhau.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Nếu mặt phẳng (α)">(α) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng phẳng (β)">(β) thì (α)">(α) và (β)">(β) song song với nhau.
- Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Lời giải chi tiết
a) Sai. (P) có thể cắt (Q).
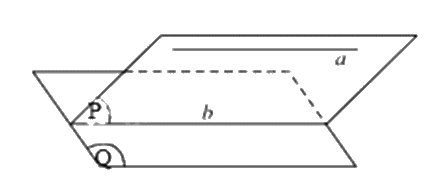
b) Sai. Cần thêm điều kiện hai đường thẳng đó cắt nhau.
c) Đúng.
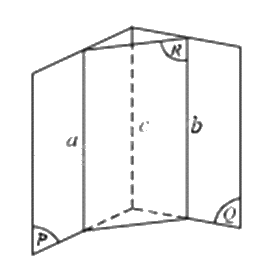
d) Sai. (P) và (Q) có thể cắt nhau.
Bài 4.21 trang 93 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức về đạo hàm, bao gồm đạo hàm của hàm số tại một điểm, đạo hàm của các hàm số cơ bản, và các quy tắc tính đạo hàm.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp học sinh lựa chọn phương pháp giải phù hợp và tránh sai sót trong quá trình giải.
(Ở đây sẽ là lời giải chi tiết của bài toán, bao gồm các bước giải, giải thích rõ ràng, và sử dụng các công thức toán học cần thiết. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh theo dõi và nắm bắt được phương pháp giải.)
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ xem xét một số ví dụ minh họa và bài tập tương tự. Các ví dụ này sẽ giúp học sinh củng cố kiến thức và kỹ năng giải bài tập về đạo hàm.
Khi giải bài tập về đạo hàm, học sinh cần lưu ý một số điểm sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Bài 4.21 trang 93 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong thực tế. Bằng cách nắm vững các khái niệm và công thức về đạo hàm, học sinh có thể giải quyết các bài tập này một cách hiệu quả và tự tin.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và hướng dẫn này sẽ giúp học sinh hiểu rõ hơn về bài tập này và đạt kết quả tốt trong học tập.