Chào mừng bạn đến với bài học về Lý thuyết Hai đường thẳng vuông góc trong chương trình Toán 11 Kết nối tri thức tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về mối quan hệ vuông góc giữa hai đường thẳng trong không gian.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, điều kiện, tính chất và các ứng dụng thực tế của hai đường thẳng vuông góc.
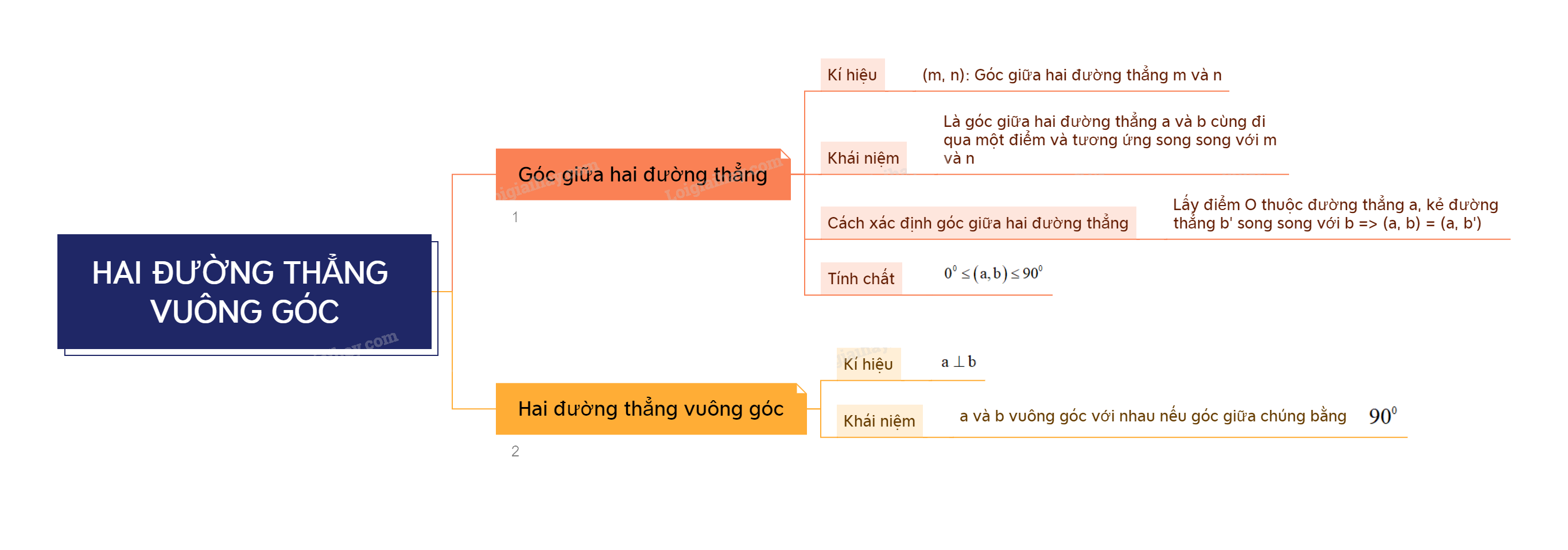
1. Góc giữa hai đường thẳng
1. Góc giữa hai đường thẳng
Góc giữa hai đường thẳng m và n trong không gian, kí hiệu (m, n), là góc giữa hai đường thẳng a và b cùng đi qua một điểm và tương ứng song song với m và n.
Chú ý:
- Để xác định góc giữa hai đường thẳng chéo nhau a và b, ta có thể lấy một điểm O thuộc đường thẳng a và qua đó kẻ đường thẳng b’ song song với b. Khi đó \(\left( {a,b} \right) = \left( {a,b'} \right)\).
- Với hai đường thẳng a, b bất kì: \({0^0} \le \left( {a,b} \right) \le {90^0}\).
2. Hai đường thẳng vuông góc
Hai đường thẳng a, b được gọi là vuông góc với nhau, kí hiệu \(a \bot b\), nếu góc giữa chúng bằng \({90^0}\).
Trong chương trình Toán 11 Kết nối tri thức, kiến thức về đường thẳng và mặt phẳng đóng vai trò nền tảng. Một trong những nội dung quan trọng nhất là lý thuyết về hai đường thẳng vuông góc. Bài viết này sẽ trình bày chi tiết lý thuyết này, kèm theo các ví dụ minh họa và bài tập để bạn có thể nắm vững kiến thức.
Hai đường thẳng được gọi là vuông góc với nhau khi góc giữa chúng bằng 90°. Ký hiệu: a ⊥ b.
Có nhiều cách để xác định hai đường thẳng vuông góc. Dưới đây là một số điều kiện quan trọng:
Hai đường thẳng vuông góc có những tính chất quan trọng sau:
Các bài tập liên quan đến hai đường thẳng vuông góc thường yêu cầu:
Ví dụ 1: Cho hai đường thẳng a và b có vector chỉ phương lần lượt là u = (1, 2, -1) và v = (2, -1, 1). Xác định xem hai đường thẳng này có vuông góc hay không?
Giải: Ta tính tích vô hướng của hai vector chỉ phương:
u.v = (1)(2) + (2)(-1) + (-1)(1) = 2 - 2 - 1 = -1 ≠ 0
Vậy hai đường thẳng a và b không vuông góc.
Ví dụ 2: Tìm giá trị của m để đường thẳng d: y = mx + 3 vuông góc với đường thẳng Δ: y = -2x + 1.
Giải: Để hai đường thẳng vuông góc, ta cần có m.(-2) = -1 ⇔ m = 1/2.
Lý thuyết về hai đường thẳng vuông góc có nhiều ứng dụng trong thực tế, đặc biệt trong các lĩnh vực như:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức đầy đủ và hữu ích về lý thuyết hai đường thẳng vuông góc trong chương trình Toán 11 Kết nối tri thức. Chúc bạn học tập tốt!