Chào mừng bạn đến với bài học về Lý thuyết Phép chiếu song song, một phần quan trọng trong chương trình Toán 11 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và cần thiết để hiểu rõ về phép chiếu song song, một công cụ quan trọng trong việc giải quyết các bài toán hình học không gian.
Chúng tôi tại giaitoan.edu.vn cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và đầy đủ, giúp bạn tự tin chinh phục môn Toán.
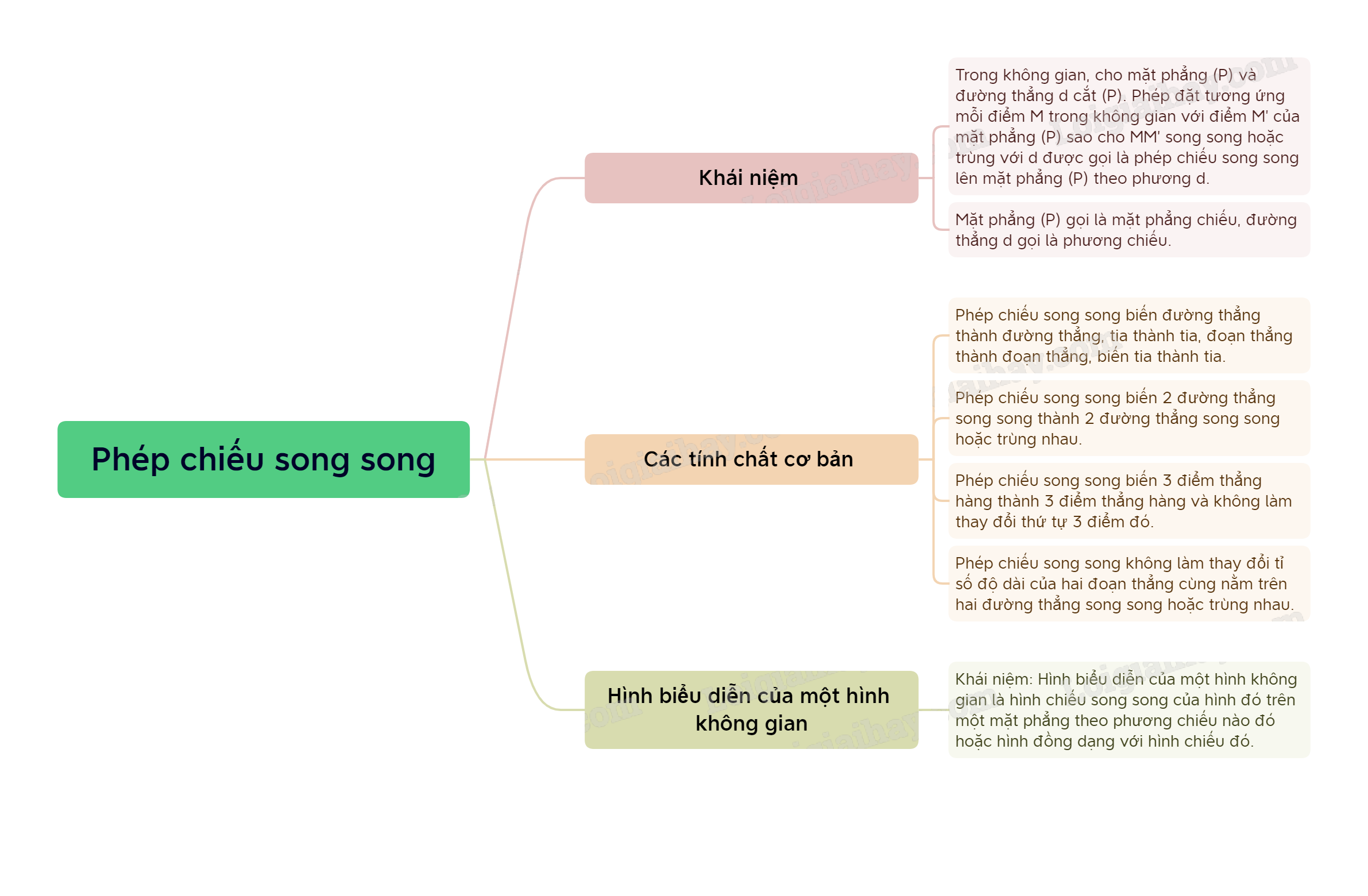
1. Phép chiếu song song
1. Phép chiếu song song
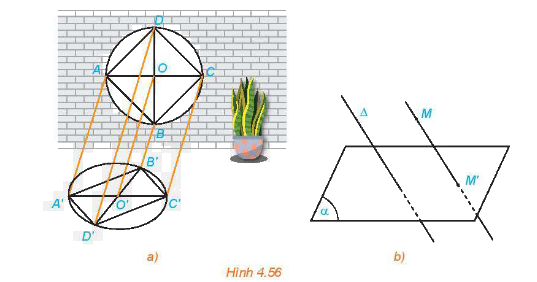
Cho mặt phẳng \(\left( \alpha \right)\)và đường thẳng \(\Delta \) cắt \(\left( \alpha \right)\). Với mỗi điểm M trong không gian ta xác định điểm M’ như sau:
- Nếu M thuộc\(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và \(\Delta \).
- Nếu M không thuộc \(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và đường thẳng qua M song song với \(\Delta \).
- Điểm M’ được gọi là hình chiếu song song của điểm M trên mặt phẳng \(\left( \alpha \right)\) theo phương \(\Delta \).
- Phép đặt tương ứng mỗi điểm M với hình chiếu M’ của nó được gọi là phép chiếu song song lên \(\left( \alpha \right)\)theo phương \(\Delta \).
- Mặt phẳng \(\left( \alpha \right)\) được gọi là mặt phẳng chiếu, phương \(\Delta \)gọi là phương chiếu.
- Cho hình \(\Re \), tập hợp các hình chiếu \(\Re '\)của các điểm M thuộc \(\Re \)qua phép chiếu song song được gọi là hình chiếu của \(\Re \) qua phép chiếu song song đó.
2. Tính chất của phép chiếu song song
- Phép chiếu song song biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi thứ tự 3 điểm đó.
- Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.
- Phép chiếu song song biến 2 đường thẳng song song thành 2 đường thẳng song song hoặc trùng nhau.
- Phép chiếu song song giữ nguyên tỉ số độ dài của hai đoạn thẳng cùng nằm trên một đường thẳng hoặc nằm trên hai đường thẳng song song.
3. Hình biểu diễn của một hình không gian
Hình biểu diễn của một hình không gian là hình chiếu song song của hình đó trên một mặt phẳng theo phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.
Phép chiếu song song là một phép biến hình quan trọng trong hình học không gian, đóng vai trò then chốt trong việc nghiên cứu và giải quyết các bài toán liên quan đến hình chiếu của các đối tượng trong không gian ba chiều lên một mặt phẳng.
Phép chiếu song song lên mặt phẳng (P) theo phương d là một phép biến hình biến mỗi điểm M trong không gian thành điểm M’ trên (P) sao cho đường thẳng MM’ song song với phương d.
Phép chiếu song song bảo toàn tỷ số giữa hai đoạn thẳng nằm trên cùng một đường thẳng.
Cụ thể, nếu M, N, P là ba điểm thẳng hàng và M’, N’, P’ là hình chiếu của chúng lên mặt phẳng (P) thì:
MN/NP = M'N'/N'P'
Một trường hợp đặc biệt của phép chiếu song song là phép chiếu vuông góc, trong đó phương d vuông góc với mặt phẳng (P).
Trong phép chiếu vuông góc, hình chiếu của một điểm là giao điểm của đường thẳng vuông góc với mặt phẳng (P) tại điểm đó và mặt phẳng (P).
Phép chiếu song song có nhiều ứng dụng trong thực tế, bao gồm:
Bài tập 1: Cho hình chóp S.ABCD. Hãy xác định hình chiếu song song của đỉnh S lên mặt phẳng (ABCD) theo phương vuông góc với (ABCD).
Bài tập 2: Cho hai đường thẳng song song a và b. Hãy chứng minh rằng hình chiếu song song của a và b lên một mặt phẳng (P) cũng là hai đường thẳng song song.
Phép chiếu song song là một khái niệm cơ bản trong hình học không gian, liên quan mật thiết đến các khái niệm khác như đường thẳng song song, mặt phẳng song song, và góc giữa đường thẳng và mặt phẳng.
Việc nắm vững lý thuyết về phép chiếu song song sẽ giúp bạn giải quyết các bài toán hình học không gian một cách hiệu quả và chính xác hơn.
Bài học về Lý thuyết Phép chiếu song song - SGK Toán 11 Kết nối tri thức đã cung cấp cho bạn những kiến thức cơ bản và quan trọng về phép chiếu song song. Hy vọng rằng, với những kiến thức này, bạn sẽ tự tin hơn trong việc học tập và giải quyết các bài toán hình học không gian.
Hãy tiếp tục luyện tập và khám phá thêm những kiến thức thú vị khác tại giaitoan.edu.vn!