Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau đi sâu vào giải chi tiết các bài tập trong mục 4, trang 75 và 76 của sách giáo khoa Toán 11 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Các hình ảnh dưới đây có đặc điểm chung nào với hình chóp tam giác đều mà em đã học ở lớp 8?
Video hướng dẫn giải
Các hình ảnh dưới đây có đặc điểm chung nào với hình chóp tam giác đều mà em đã học ở lớp 8?

Phương pháp giải:
Dựa vào tính chất của hình chóp tam giác đều để so sánh.
Lời giải chi tiết:
- Các cạnh bên đều bằng nhau.
- Các mặt bên của hình chóp này là tam giác cân.
- Chân đường cao trung với tâm đáy.
- Góc được tạo bởi mặt bên và mặt đáy đều bằng nhau.
- Góc được tạo bởi cạnh bên và mặt đáy đều bằng nhau.
Video hướng dẫn giải
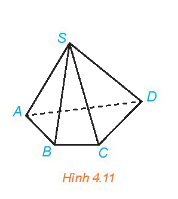
Cho hình chóp S.ABCD. Gọi tên các mặt bên và mặt đáy của hình chóp đó.
Phương pháp giải:
Hình chóp là một hình không gian gồm có một đa giác gọi là mặt đáy, các tam giác chung đỉnh gọi là mặt bên, đỉnh chung của các mặt bên đó gọi là đỉnh của hình chóp (h.2.4)

Lời giải chi tiết:
- Các mặt bên: (SAB), (SBC), (SCD), (SAD).
- Mặt đáy: ABCD.
Video hướng dẫn giải
Trong các hình chóp ở HĐ7, hình chóp nào có ít mặt nhất? Xác định số cạnh và số mặt của hình chóp đó.
Phương pháp giải:
Quan sát các hình chóp, ta có thể đếm được số mặt và cạnh.
Lời giải chi tiết:
Hình thứ ba có ít mặt nhất. Có 4 mặt và 6 cạnh.
Video hướng dẫn giải
Trong Ví dụ 6, xác định giao điểm của đường thẳng DF và mặt phẳng (ABC).
Phương pháp giải:
Để xác định giao điểm của một đường thẳng và một mặt phẳng, ta có thể tìm giao điểm của đường thẳng đó với một đường thẳng nằm trong mặt phẳng đã cho.
Lời giải chi tiết:

Xét trong mp(BCD) ta có: DE cắt BC tại K.
Xét trong mp(ADK) ta có: DF cắt AK tại H.
Như vậy, H thuộc đường thẳng DF và AK mà AK nằm trong mp(ABC) suy ra H cũng nằm trong mp(ABC).
Do đó, H là giao điểm của DF và mp(ABC).
Mục 4 của chương trình Toán 11 tập 1 - Kết nối tri thức tập trung vào các kiến thức về vectơ trong không gian. Các bài tập trang 75 và 76 SGK yêu cầu học sinh vận dụng các định nghĩa, tính chất của vectơ, các phép toán vectơ (cộng, trừ, nhân với một số thực) và các ứng dụng của vectơ trong việc giải quyết các bài toán hình học không gian.
Bài tập này yêu cầu học sinh xác định vectơ chỉ phương và vectơ pháp tuyến của một đường thẳng cho trước. Để làm được bài này, học sinh cần nắm vững định nghĩa của vectơ chỉ phương và vectơ pháp tuyến, cũng như các phương pháp tìm vectơ trong không gian.
Ví dụ:
Bài tập này yêu cầu học sinh xác định vị trí tương đối giữa hai đường thẳng (song song, cắt nhau, chéo nhau). Để làm được bài này, học sinh cần nắm vững các điều kiện để hai đường thẳng song song, cắt nhau hoặc chéo nhau.
Ví dụ:
Cho hai đường thẳng:
Xác định vị trí tương đối giữa d1 và d2.
Giải: Ta tìm được vectơ chỉ phương của d1 là a = (1; -1; 2) và vectơ chỉ phương của d2 là b = (-1; 1; -1). Ta thấy a và b không cùng phương. Điểm A(1; 2; 3) thuộc d1 và điểm B(2; 1; 4) thuộc d2. Vectơ AB = (1; -1; 1). Ta kiểm tra xem AB có cùng phương với a và b hay không. Vì AB không cùng phương với a và b nên hai đường thẳng d1 và d2 chéo nhau.
Bài tập này yêu cầu học sinh tính góc giữa hai đường thẳng. Để làm được bài này, học sinh cần nắm vững công thức tính góc giữa hai đường thẳng và các phép toán vectơ.
Công thức tính góc θ giữa hai đường thẳng d1 và d2 có vectơ chỉ phương lần lượt là a và b là:
cos θ = |a.b| / (||a||.||b||)
Bài tập này yêu cầu học sinh tính khoảng cách giữa hai đường thẳng chéo nhau. Để làm được bài này, học sinh cần nắm vững công thức tính khoảng cách giữa hai đường thẳng chéo nhau và các phép toán vectơ.
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau để nắm vững kiến thức về vectơ trong không gian:
Hy vọng với những giải thích chi tiết và ví dụ minh họa trên, các em học sinh đã hiểu rõ cách giải các bài tập trong mục 4 trang 75, 76 SGK Toán 11 tập 1 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!