Bài 8 trang 105 SGK Toán 11 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bài tập này yêu cầu học sinh vận dụng các công thức và quy tắc đạo hàm đã học để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 8 trang 105, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho đồ thị ba hàm số mũ (y = {a^x},y = {b^x}) và (y = {c^x}) như trong hình vẽ dưới đây
Đề bài
Cho đồ thị ba hàm số mũ \(y = {a^x},y = {b^x}\) và \(y = {c^x}\) như trong hình vẽ dưới đây. Khẳng định nào sau đây là đúng?
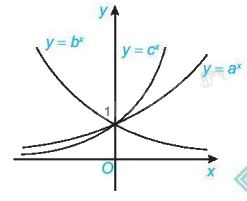
A. \(a > c > b\).
B. \(b > a > c\).
C. \(c > a > b\).
D. \(c > b > a\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Đồ thị hàm số \(y = {a^x}\) đồng biến nếu \(a > 1\)
Đồ thị hàm số \(y = {a^x}\) nghịch biến nếu \(0 < a < 1\)
Lời giải chi tiết
Đồ thị hàm số \(y = {b^x}\) nghịch biến nên \(0 < b < 1\)
Đồ thị hàm số \(y = {a^x},y = {c^x}\) đồng biến nên \(a,c > 1\)
Với \(x > 0\) bất kì ta có \({c^x} > {a^x} \Leftrightarrow c > a\)
Đáp án C
Bài 8 trang 105 SGK Toán 11 tập 2 - Kết nối tri thức tập trung vào việc tính đạo hàm của hàm số lượng giác và hàm hợp. Để giải quyết bài tập này, học sinh cần nắm vững các công thức đạo hàm cơ bản của các hàm số lượng giác như sinx, cosx, tanx, cotx, cũng như quy tắc đạo hàm của hàm hợp.
Trước khi đi vào giải bài tập, chúng ta cùng ôn lại một số kiến thức lý thuyết quan trọng:
Bài 8 thường bao gồm nhiều câu nhỏ, mỗi câu yêu cầu tính đạo hàm của một hàm số khác nhau. Dưới đây là hướng dẫn giải chi tiết cho từng câu:
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = cos(2x + 1) * (2x + 1)' = 2cos(2x + 1)
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = -sin(x2) * (x2)' = -2xsin(x2)
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = (1/cos2(3x - 2)) * (3x - 2)' = 3/cos2(3x - 2)
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = (-1/sin2(x/2)) * (x/2)' = -1/(2sin2(x/2))
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự sau:
Khi giải các bài tập về đạo hàm hàm số lượng giác, bạn cần lưu ý những điều sau:
Hy vọng với hướng dẫn chi tiết này, bạn đã hiểu rõ cách giải Bài 8 trang 105 SGK Toán 11 tập 2 - Kết nối tri thức. Chúc bạn học tập tốt!
| Hàm số | Đạo hàm |
|---|---|
| y = sin(2x + 1) | y' = 2cos(2x + 1) |
| y = cos(x2) | y' = -2xsin(x2) |