Bài 7.23 trang 59 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, BC = c.
Đề bài
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, BC = c.
a) Tính khoảng cách giữa CC' và (BB'D'D).
b) Xác định đường vuông góc chung và tính khoảng cách giữa AC và B'D'.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P).
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song, tương ứng chứa hai đường thẳng đó.
Lời giải chi tiết
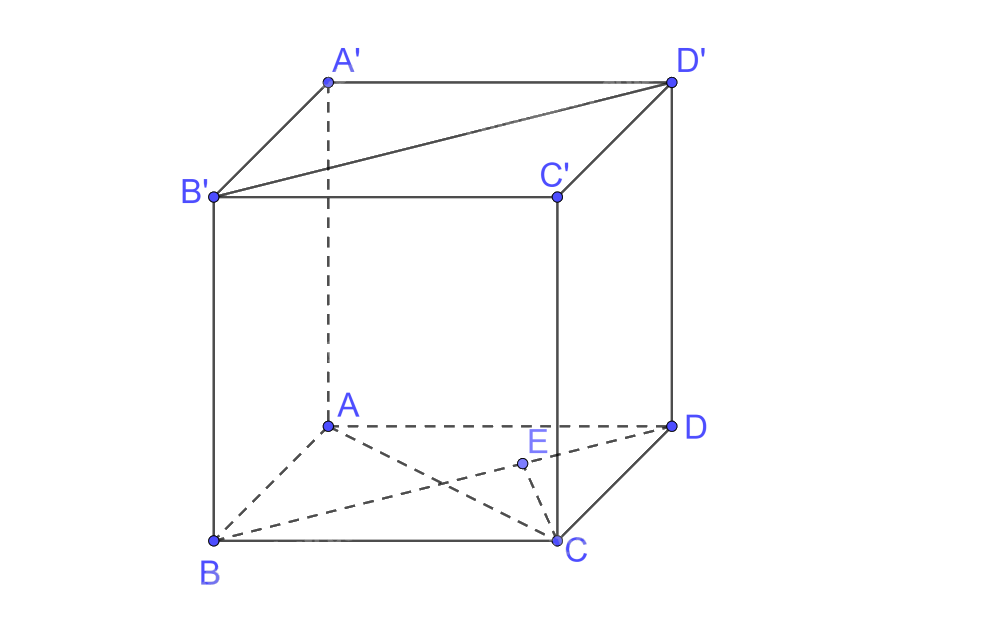
a) Trong (ABCD) kẻ \(CE \bot BD\)
Mà \(CE \bot BB'\left( {BB' \bot \left( {ABCD} \right)} \right) \Rightarrow CE \bot \left( {BB'D'D} \right)\)
Ta có CC’ // BB’ \( \Rightarrow \) CC’ // (BB’D’D) \( \Rightarrow \) d(CC’, (BB’D’D)) = d(C, (BB’D’D)) = CE
Xét tam giác BCD vuông tại C có
\(\frac{1}{{C{E^2}}} = \frac{1}{{B{C^2}}} + \frac{1}{{C{D^2}}} = \frac{1}{{{c^2}}} + \frac{1}{{{b^2}}} = \frac{{{b^2} + {c^2}}}{{{c^2}{b^2}}} \Rightarrow CE = \frac{{bc}}{{\sqrt {{b^2} + {c^2}} }}\)
b) \(AC \subset \left( {ABCD} \right),B'D' \subset \left( {A'B'C'D'} \right),\left( {ABCD} \right)//\left( {A'B'C'D'} \right)\)
\( \Rightarrow d\left( {AC,B'D'} \right) = d\left( {\left( {ABCD} \right),\left( {A'B'C'D'} \right)} \right) = BB' = a\)
Bài 7.23 SGK Toán 11 tập 2 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến ứng dụng của đạo hàm trong việc tìm cực trị của hàm số. Cụ thể, bài toán thường cho một hàm số và yêu cầu tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
Để giải bài toán này, học sinh cần nắm vững các kiến thức sau:
(Ở đây sẽ là lời giải chi tiết của bài toán, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Lời giải sẽ được trình bày chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải toán.)
Ví dụ, giả sử bài toán yêu cầu tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x3 - 3x2 + 2 trên đoạn [-1; 3].
Để củng cố kiến thức và kỹ năng giải toán, học sinh có thể luyện tập thêm các bài tập tương tự trong SGK Toán 11 tập 2 Kết nối tri thức và các tài liệu tham khảo khác.
Các bài tập tương tự:
Lưu ý: Khi giải các bài toán về ứng dụng của đạo hàm, học sinh cần chú ý đến điều kiện của bài toán và lựa chọn phương pháp giải phù hợp.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về Bài 7.23 trang 59 SGK Toán 11 tập 2 - Kết nối tri thức và có thể tự tin giải quyết các bài toán tương tự.