Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 5 trang 28 và 29 sách giáo khoa Toán 11 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hàm số \(y = \tan x\) a) Xét tính chẵn, lẻ của hàm số
Cho hàm số \(y = \tan x\)
a) Xét tính chẵn, lẻ của hàm số
b) Hoàn thành bảng giá trị của hàm số \(y = \tan x\) trên khoảng\(\;\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
\(x\) | \( - \frac{\pi }{3}\) | \( - \frac{\pi }{4}\) | \( - \frac{\pi }{6}\) | 0 | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) |
\(y = \tan x\) | ? | ? | ? | ? | ? | ? | ? |
Bằng cách lấy nhiều điểm \(M\left( {x;\tan x} \right)\) với \(x \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) và nối lại ta được đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kỳ \(T = \pi \), ta được đồ thị của hàm số \(y = \tan x\) như hình dưới đây.
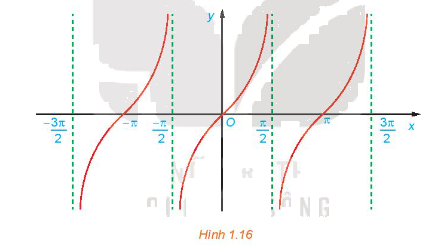
Từ đồ thị ở Hình 1.16, hãy tìm tập giá trị và các khoảng đồng biến của hàm số \(y = \tan x\).
Phương pháp giải:
Sử dụng định nghĩa hàm số chẵn lẻ
Dựa vào đồ thị để xác định tập giá trị, các khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
a) Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \tan \left( { - x} \right) = - \tan x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \tan x\) là hàm số lẻ.
b)
\(x\) | \( - \frac{\pi }{3}\) | \( - \frac{\pi }{4}\) | \( - \frac{\pi }{6}\) | \(0\) | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) |
\(\tan x\) | \( - \sqrt 3 \) | \( - 1\) | \( - \frac{{\sqrt 3 }}{3}\) | \(0\) | \(\frac{{\sqrt 3 }}{3}\) | \(1\) | \(\sqrt 3 \) |
c) Từ đồ thị trên, ta thấy hàm số \(y = \tan x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\), tập giá trị là \(\mathbb{R}\) và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\).
Sử dụng đồ thị đã vẽ ở Hình 1.16, hãy xác định các giá trị của x trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\) để hàm số \(y = \tan x\) nhận giá trị âm.
Phương pháp giải:
Nhìn đồ thị để xác định vị trí của y và x
Lời giải chi tiết:
Hàm số nhận giá trị âm ứng với phần đồ thị nằm dưới trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\), thì \(y < 0\) khi \(x\; \in \left( { - \frac{\pi }{2};0} \right) \cup \left( {\frac{\pi }{2};\;\pi } \right)\)
Mục 5 của SGK Toán 11 tập 1 chương trình Kết nối tri thức tập trung vào các kiến thức về vectơ trong không gian. Cụ thể, các em sẽ được làm quen với các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các ứng dụng của vectơ trong việc giải quyết các bài toán hình học không gian.
Mục 5 bao gồm các nội dung chính sau:
Bài tập này yêu cầu các em tìm vectơ chỉ phương của đường thẳng cho trước. Để giải bài tập này, các em cần nắm vững khái niệm vectơ chỉ phương và cách xác định vectơ chỉ phương từ phương trình đường thẳng.
Ví dụ: Cho đường thẳng d có phương trình tham số: x = 1 + 2t y = -1 + t z = 3 - t
Vectơ chỉ phương của đường thẳng d là a = (2; 1; -1).
Bài tập này yêu cầu các em xác định vị trí tương đối của hai đường thẳng cho trước (song song, cắt nhau, chéo nhau). Để giải bài tập này, các em cần nắm vững các điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau.
Ví dụ: Cho hai đường thẳng d1 và d2 có phương trình:
d1: x = 1 + t y = 2 - t z = 3 + 2t
d2: x = 2 + 2t y = 1 - 2t z = 5 + 4t
Để xác định vị trí tương đối của hai đường thẳng này, ta xét vectơ chỉ phương của mỗi đường thẳng và một điểm thuộc mỗi đường thẳng. Nếu hai vectơ chỉ phương cùng phương và một điểm thuộc đường thẳng này không thuộc đường thẳng kia thì hai đường thẳng song song. Nếu hai vectơ chỉ phương không cùng phương và hai đường thẳng có một điểm chung thì hai đường thẳng cắt nhau. Nếu hai vectơ chỉ phương không cùng phương và hai đường thẳng không có điểm chung thì hai đường thẳng chéo nhau.
Bài tập này yêu cầu các em tính góc giữa hai vectơ cho trước. Để giải bài tập này, các em cần nắm vững công thức tính góc giữa hai vectơ: cos(α) = (a.b) / (|a||b|), trong đó a và b là hai vectơ, a.b là tích vô hướng của hai vectơ, |a| và |b| là độ dài của hai vectơ.
Ví dụ: Cho hai vectơ a = (1; 2; 3) và b = (-1; 0; 1). Tính góc α giữa hai vectơ a và b.
Ta có: a.b = 1*(-1) + 2*0 + 3*1 = 2 |a| = √(1^2 + 2^2 + 3^2) = √14 |b| = √((-1)^2 + 0^2 + 1^2) = √2
cos(α) = 2 / (√14 * √2) = 2 / √28 = 2 / (2√7) = 1/√7
α = arccos(1/√7) ≈ 69.3°
Hy vọng với những giải thích chi tiết và ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải các bài tập về vectơ trong không gian. Chúc các em học tập tốt!