Giải Bài 3.3 trang 61 SGK Toán 11 tập 1 - Kết nối tri thức

Bài 3.3 trang 61 SGK Toán 11 tập 1 - Kết nối tri thức

Bài 3.3 trang 61 SGK Toán 11 tập 1 thuộc chương 1: Hàm số và đồ thị. Bài học này tập trung vào việc giải quyết các bài toán liên quan đến hàm số bậc hai, bao gồm xác định hệ số, tìm đỉnh parabol, và vẽ đồ thị hàm số.

Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

Thời gian ra sân (giờ) của một số cựu cầu thủ ở giải ngoại hạng Anh qua các thời kì được cho như sau: 653 632 609 572 565 535 516 514 508 505 504 504 503 499 496 492 (Theo: https://www.premierleague.com/) Hãy chuyển mẫu số liệu trên sang dạng ghép nhóm với bảy nhóm có độ dài bằng nhau

Đề bài

Thời gian ra sân (giờ) của một số cựu cầu thủ ở giải ngoại hạng Anh qua các thời kì được cho như sau:

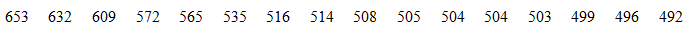Bài 3.3 trang 61 SGK Toán 11 tập 1 - Kết nối tri thức 1 (Theo: https://www.premierleague.com/)

Hãy chuyển mẫu số liệu trên sang dạng ghép nhóm với bảy nhóm có độ dài bằng nhau

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Bài 3.3 trang 61 SGK Toán 11 tập 1 - Kết nối tri thức 2

Để chuyển mẫu số liệu không ghép nhóm sang mẫu số liệu ghép nhóm, ta làm như sau:

Bước 1: Chia miền giá trị của mẫu số liệu thành một số nhóm theo tiêu chí cho trước.

Bước 2: Đếm số giá trị của mẫu số liệu thuộc mỗi nhóm (tần số) và lập bảng thống kê cho mẫu số liệu ghép.

Lời giải chi tiết

Giá trị lớn nhất là: 653.

Giá trị bé nhất là: 492.

Khoảng biến thiên là: 653 - 492 = 161.

Để chia thành 7 nhóm có độ dài bằng nhau, ta lấy điểm đầu mút trái của nhóm đầu tiên là 492, điểm đầu mút phải của nhóm cuối là 653 với độ dài mỗi nhóm là 23.

Ta có mẫu số liệu ghép nhóm sau:

Bài 3.3 trang 61 SGK Toán 11 tập 1 - Kết nối tri thức 3

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Bài 3.3 trang 61 SGK Toán 11 tập 1 - Kết nối tri thức – hành trang không thể thiếu trong chuyên mục Đề thi Toán lớp 11 trên nền tảng đề thi toán. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Bài 3.3 trang 61 SGK Toán 11 tập 1 - Kết nối tri thức: Giải chi tiết và hướng dẫn

Bài 3.3 trang 61 SGK Toán 11 tập 1 - Kết nối tri thức là một phần quan trọng trong chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về hàm số bậc hai vào giải quyết các bài toán thực tế. Để hiểu rõ hơn về nội dung này, chúng ta sẽ cùng nhau phân tích từng phần của bài tập.

1. Tóm tắt lý thuyết cần nắm vững

Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức cơ bản về hàm số bậc hai:

Dạng tổng quát của hàm số bậc hai: y = ax² + bx + c (a ≠ 0)
Đỉnh của parabol: I(-b/2a, -Δ/4a) với Δ = b² - 4ac
Trục đối xứng của parabol: x = -b/2a
Hệ số a quyết định chiều mở của parabol: a > 0: parabol mở lên trên; a < 0: parabol mở xuống dưới

2. Giải chi tiết Bài 3.3 trang 61 SGK Toán 11 tập 1 - Kết nối tri thức

Bài 3.3: Xác định a, b, c của hàm số sau:

a) y = 2x² - 5x + 1
b) y = -x² + 3x
c) y = 4x - x² + 2

Giải:

a) y = 2x² - 5x + 1: a = 2, b = -5, c = 1
b) y = -x² + 3x: a = -1, b = 3, c = 0
c) y = 4x - x² + 2: y = -x² + 4x + 2; a = -1, b = 4, c = 2

3. Bài tập vận dụng và mở rộng

Để củng cố kiến thức, các em có thể tự giải các bài tập sau:

Bài 3.4 trang 61 SGK Toán 11 tập 1 - Kết nối tri thức: Tìm đỉnh của parabol y = x² - 4x + 3
Bài 3.5 trang 62 SGK Toán 11 tập 1 - Kết nối tri thức: Vẽ đồ thị hàm số y = 2x² + x - 1

4. Lưu ý khi giải bài tập về hàm số bậc hai

Khi giải các bài tập về hàm số bậc hai, các em cần chú ý:

Xác định đúng hệ số a, b, c: Đây là bước quan trọng để xác định các yếu tố của parabol.
Sử dụng công thức chính xác: Công thức tính đỉnh, trục đối xứng, và nghiệm của phương trình bậc hai cần được sử dụng chính xác.
Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

5. Ứng dụng của hàm số bậc hai trong thực tế

Hàm số bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:

Tính quỹ đạo của vật ném: Quỹ đạo của một vật ném lên không trung có thể được mô tả bằng một hàm số bậc hai.
Thiết kế cầu: Hình dạng của một cầu có thể được mô tả bằng một hàm số bậc hai.
Phân tích dữ liệu kinh tế: Hàm số bậc hai có thể được sử dụng để mô tả sự thay đổi của các chỉ số kinh tế.

Hy vọng với bài giải chi tiết và hướng dẫn này, các em sẽ hiểu rõ hơn về Bài 3.3 trang 61 SGK Toán 11 tập 1 - Kết nối tri thức và có thể tự tin giải các bài tập tương tự. Chúc các em học tốt!