Bài 3.13 trang 69 SGK Toán 11 tập 1 thuộc chương 1: Hàm số lượng giác và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số lượng giác, đặc biệt là hàm cosin, để giải quyết các bài toán thực tế.
giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
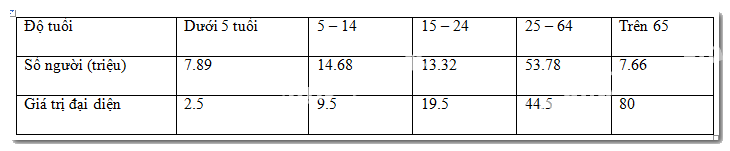
Cơ cấu dân số Việt Nam năm 2020 theo độ tuổi được cho trong bảng sau: Độ tuổi Dưới 5 tuổi (5 - 14) (15 - 24) (25 - 64) Trên 65 Số người (triệu) (7,89) (14,68) (13,32) (53,78) (7,66) (Theo: http://ourworldindata.org) Chọn 80 là giá trị đại diện cho nhóm trên 65 tuổi. Tính tuổi trung bình của người Việt Nam năm 2020.
Đề bài
Cơ cấu dân số Việt Nam năm 2020 theo độ tuổi được cho trong bảng sau:

(Theo: http://ourworldindata.org)
Chọn 80 là giá trị đại diện cho nhóm trên 65 tuổi. Tính tuổi trung bình của người Việt Nam năm 2020.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng công thức số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\bar x\).
\(\bar x = \frac{{{m_1}{x_1} + \ldots + {m_k}{x_k}}}{n}\)
Trong đó \(n = {m_1} + \ldots + {m_k}\) là cỡ mẫu và là giá trị đại diện của nhóm \(\left[ {{a_i},{a_{i + 1}}} \right)\).
Lời giải chi tiết
Tuổi trung bình của người Việt Nam năm 2020:
\(\bar x = \frac{{7.,89 \times 2,5 + 14,68 \times 9,5 + 13,32 \times 19,5 + 53,78 \times 44,5 + 7,66 \times 80}}{{7,89 + 14,68 + 13,32 + 53,78 + 7,66}} = 35,19\).
Bài 3.13 trang 69 SGK Toán 11 tập 1 - Kết nối tri thức yêu cầu chúng ta xét một tình huống thực tế liên quan đến việc đo chiều cao của một ngọn núi. Bài toán này giúp học sinh hiểu rõ hơn về ứng dụng của hàm cosin trong việc giải quyết các vấn đề thực tế.
Để giải bài toán này, chúng ta cần hiểu rõ các yếu tố sau:
Chúng ta có thể sử dụng hàm cosin để thiết lập mối quan hệ giữa góc quan sát, khoảng cách và chiều cao của núi.
Giả sử góc quan sát là α, khoảng cách từ người quan sát đến chân núi là d, và chiều cao của núi là h. Ta có:
tan(α) = h / d
Từ đó, ta có thể tính chiều cao của núi như sau:
h = d * tan(α)
Giả sử góc quan sát α = 30 độ và khoảng cách từ người quan sát đến chân núi d = 100 mét. Khi đó, chiều cao của núi là:
h = 100 * tan(30°) = 100 * (1/√3) ≈ 57.74 mét
Khi giải bài toán này, cần chú ý đến đơn vị đo lường và đảm bảo rằng tất cả các đại lượng đều được biểu diễn trong cùng một đơn vị. Ngoài ra, cần kiểm tra lại kết quả để đảm bảo tính hợp lý.
Bài toán này có thể được mở rộng bằng cách xét các trường hợp khác nhau, chẳng hạn như khi người quan sát đứng ở một vị trí khác hoặc khi góc quan sát thay đổi. Việc giải quyết các bài toán mở rộng này sẽ giúp học sinh hiểu sâu hơn về ứng dụng của hàm cosin trong thực tế.
Để rèn luyện kỹ năng giải toán, học sinh có thể tự giải các bài tập tương tự, chẳng hạn như:
Bài 3.13 trang 69 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về ứng dụng của hàm cosin trong việc giải quyết các bài toán thực tế. Bằng cách nắm vững kiến thức và rèn luyện kỹ năng giải toán, học sinh có thể tự tin đối mặt với các bài toán tương tự trong các kỳ thi.
giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài toán và đạt kết quả tốt trong học tập.
Để hiểu rõ hơn về các khái niệm liên quan, các em có thể tham khảo thêm các tài liệu học tập khác, chẳng hạn như sách giáo khoa, sách bài tập, và các trang web học toán trực tuyến.
Chúc các em học tập tốt!