Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK Toán 11 Kết nối tri thức, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 1 trang 38, 39, 40 của SGK Toán 11 tập 2. Các em hãy chuẩn bị sách giáo khoa và cùng chúng tôi bắt đầu nhé!
Trên sân phẳng có một cây cột thẳng vuông góc với mặt sân.
Video hướng dẫn giải
Trên sân phẳng có một cây cột thẳng vuông góc với mặt sân.
a) Dưới ánh sáng mặt trời, bóng của cây cột trên sân có thể được nhìn như là hình chiếu của cây cột qua phép chiếu song song hay không?
b) Khi tia sáng mặt trời vuông góc với mặt sân, liệu ta có thể quan sát được bóng của cây cột trên sân hay không?
Phương pháp giải:
Quan sát thực tế
Lời giải chi tiết:
a) Bóng của cây cột trên sân có thể được nhìn như là hình chiếu của cây cột qua phép chiếu song song với tia nắng mặt trời.
b) Khi tia sáng mặt trời vuông góc với mặt sân, bóng của cây cột sẽ không xuất hiện trên mặt sân vì không có tia sáng nào có thể chiếu trực tiếp lên bề mặt sân để tạo ra bóng của cây cột.
Video hướng dẫn giải
a) Nếu A là một điểm không thuộc mặt phẳng (P) và A’ là hình chiếu của A trên (P) thì đường thẳng AA’ có quan hệ gì với mặt phẳng (P)?
b) Nếu đường thẳng a vuông góc với mặt phẳng (P) thì hình chiếu của a trên (P) là gì?
Phương pháp giải:
Phép chiếu song song lên mặt phẳng (P) theo phương \(\Delta \) vuông góc với (P) được gọi là phép chiếu vuông góc lên mặt phẳng (P).
Lời giải chi tiết:
a) AA’ vuông góc với mặt phẳng (P)
b) Nếu đường thẳng a vuông góc với mặt phẳng (P) thì hình chiếu của a trên (P) là giao điểm của a với (P).
Video hướng dẫn giải
Cho đường thẳng a và mặt phẳng (P) không vuông góc với nhau. Xét b là một đường thẳng nằm trong (P). Trên a, lấy hai điểm M, N tuỳ ý. Gọi M', N' tương ứng là hình chiếu của M, N trên mặt phẳng (P) (H.7.34).
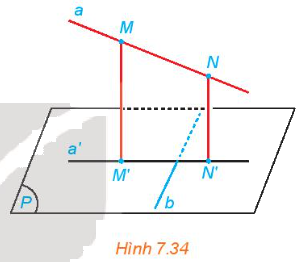
a) Hình chiếu của a trên mặt phẳng (P) là đường thẳng nào?
b) Nếu b vuông góc với M'N' thì b có vuông góc với a hay không?
c) Nếu b vuông góc với a thì b có vuông góc với M'N' hay không?
Phương pháp giải:
Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với 2 đường thẳng cắt nhau nằm trong mặt phẳng đó.
Lời giải chi tiết:
a) Vì M', N' tương ứng là hình chiếu của M, N trên mặt phẳng (P) nên hình chiếu của a trên mặt phẳng (P) là a’ đường thẳng đi qua hai điểm M', N'.
b) b vuông góc với M'N' và b vuông góc với MM' (do M' là hình chiếu của M trên (P)); M'N' cắt MM' tại M' do đó b vuông góc mặt phẳng tạo bởi M'N', MM' suy ra b có vuông góc với a.
c) b vuông góc với a và b vuông góc với MM' (do M' là hình chiếu của M trên (P)); a cắt MM' tại M do đó b vuông góc mặt phẳng tạo bởi a, MM' suy ra b có vuông góc với M'N'.
Video hướng dẫn giải
Cho hình chóp S.ABC có SA = SB = SC. Gọi O là hình chiếu của S trên mặt phẳng (ABC) (H.7.36).

a) Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác ABC.
b) Xác định hình chiếu của đường thẳng SA trên mặt phẳng (ABC).
c) Chứng minh rằng nếu \(AO \bot BC\) thì \(SA \bot BC.\)
d) Xác định hình chiếu của các tam giác SBC, SCA, SAB trên mặt phẳng (ABC)
Phương pháp giải:
- Sử dụng định lý Pytago
- Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.
Lời giải chi tiết:
a) O là hình chiếu của S trên mặt phẳng (ABC) nên \(SO \bot \left( {ABC} \right)\)
Mà \(OA,OB,OC \subset \left( {ABC} \right) \Rightarrow SO \bot OA,SO \bot OB,SO \bot OC\)
Xét tam giác SAO vuông tại O \(\left( {SO \bot OA} \right)\) có
\(S{A^2} = O{A^2} + S{O^2}\) (Định lí Pytago)
Xét tam giác SBO vuông tại O \(\left( {SO \bot OB} \right)\) có
\(S{B^2} = O{B^2} + S{O^2}\) (Định lí Pytago)
Xét tam giác SCO vuông tại O \(\left( {SO \bot OC} \right)\) có
\(S{C^2} = O{C^2} + S{O^2}\) (Định lí Pytago)
Mà SA = SB = SC nên OA = OB = OC
Do đó O là tâm đường trọn ngoại tiếp tam giác ABC.
b) O là hình chiếu của S trên mặt phẳng (ABC)
A là hình chiếu của A trên mặt phẳng (ABC)
\( \Rightarrow \) OA là hình chiếu của SA trên mặt phẳng (ABC)
c) \(\left. \begin{array}{l}AO \bot BC\\SO \bot BC\left( {SO \bot \left( {ABC} \right)} \right)\\AO \cap SO = \left\{ O \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAO} \right);SA \subset \left( {SAO} \right) \Rightarrow SA \bot BC\)
d) O là hình chiếu của S trên mặt phẳng (ABC)
A là hình chiếu của A trên mặt phẳng (ABC)
B là hình chiếu của B trên mặt phẳng (ABC)
C là hình chiếu của C trên mặt phẳng (ABC)
\( \Rightarrow \) Tam giác OAB là hình chiếu của tam giác SAB trên mặt phẳng (ABC)
Tam giác OBC là hình chiếu của tam giác SBC trên mặt phẳng (ABC)
Tam giác OCA là hình chiếu của tam giác SCA trên mặt phẳng (ABC)
Mục 1 của SGK Toán 11 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa kiến thức về phép biến hình. Cụ thể, các em sẽ được củng cố các kiến thức về phép dời hình, phép đối xứng trục, phép đối xứng tâm và phép quay. Việc nắm vững các kiến thức này là nền tảng quan trọng để giải quyết các bài toán hình học trong chương trình học.
Bài tập này yêu cầu các em xác định xem một phép biến hình cho trước có phải là phép dời hình hay không. Để làm được điều này, các em cần nhớ lại định nghĩa của phép dời hình: một phép biến hình được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm bất kỳ.
Ví dụ, cho hai điểm A và B. Nếu sau khi thực hiện phép biến hình, khoảng cách giữa A' và B' (ảnh của A và B qua phép biến hình) bằng khoảng cách giữa A và B, thì phép biến hình đó là phép dời hình.
Bài tập này tập trung vào việc tìm ảnh của một điểm, một đường thẳng hoặc một hình qua phép đối xứng trục. Các em cần nắm vững tính chất của phép đối xứng trục: ảnh của một điểm qua phép đối xứng trục là điểm đối xứng của nó qua trục đó.
Để tìm ảnh của một đường thẳng qua phép đối xứng trục, các em có thể tìm ảnh của hai điểm thuộc đường thẳng đó và vẽ đường thẳng đi qua hai điểm ảnh này.
Tương tự như phép đối xứng trục, bài tập này yêu cầu các em tìm ảnh của một điểm, một đường thẳng hoặc một hình qua phép đối xứng tâm. Các em cần nhớ rằng ảnh của một điểm qua phép đối xứng tâm là điểm đối xứng của nó qua tâm đó.
Bài tập này liên quan đến việc tìm ảnh của một điểm qua phép quay. Các em cần xác định tâm quay, góc quay và chiều quay. Ảnh của một điểm qua phép quay là điểm sao cho khoảng cách từ điểm đó đến tâm quay bằng khoảng cách từ điểm gốc đến tâm quay, và góc giữa đoạn thẳng nối điểm gốc với tâm quay và đoạn thẳng nối điểm ảnh với tâm quay bằng góc quay.
Phép biến hình có rất nhiều ứng dụng trong thực tế, chẳng hạn như trong thiết kế đồ họa, kiến trúc, robot học và nhiều lĩnh vực khác. Ví dụ, trong thiết kế đồ họa, phép biến hình được sử dụng để tạo ra các hiệu ứng đặc biệt, như xoay, lật, và co giãn hình ảnh.
Để củng cố kiến thức và kỹ năng giải bài tập, các em nên luyện tập thêm với các bài tập tương tự trong sách bài tập và các đề thi thử. Giaitoan.edu.vn sẽ tiếp tục cập nhật thêm nhiều bài giải và tài liệu học tập hữu ích cho các em.
Hy vọng rằng với bài giải chi tiết và hướng dẫn cụ thể này, các em sẽ hiểu rõ hơn về các bài tập trong mục 1 trang 38, 39, 40 SGK Toán 11 tập 2 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao!