Phương trình lượng giác là một trong những chủ đề quan trọng của chương trình Toán 11 Kết nối tri thức. Việc nắm vững lý thuyết và phương pháp giải các phương trình lượng giác cơ bản là điều kiện cần thiết để giải quyết các bài toán phức tạp hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu về lý thuyết Phương trình lượng giác cơ bản, giúp bạn xây dựng nền tảng vững chắc cho môn Toán.
1. Khái niệm phương trình tương đương
1. Khái niệm phương trình tương đương
Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.
Nếu phương trình f(x) =0 tương đương với phương trình g(x) =0 thì ta viết \(f(x) = 0 \Leftrightarrow g(x) = 0\)
*Chú ý: Hai phương trình vô nghiệm là hai phương trình tương đương.
2. Phương trình \({\mathop{\rm s}\nolimits} {\rm{inx}} = m\)
Phương trình sinx=m có nghiệm khi và chỉ khi \(\left| m \right| \le 1\).
Khi \(\left| m \right| \le 1\)sẽ tồn tại duy nhất \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) thoả mãn \(\sin \alpha = m\). Khi đó:
\({\mathop{\rm s}\nolimits} {\rm{inx}} = m \Leftrightarrow \sin x = \sin \alpha \) \( \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
* Chú ý:
a, Nếu số đo của góc \(\alpha \)được cho bằng đơn vị độ thì \(\sin x = \sin {\alpha ^o} \Leftrightarrow \left[ \begin{array}{l}x = {\alpha ^o} + k{360^o}\\x = {180^o} - {\alpha ^o} + k{360^o}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
b,Một số trường hợp đặc biệt
\(\begin{array}{l}\sin x = 0 \Leftrightarrow x = k\pi ,k \in \mathbb{Z}.\\\sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}.\\\sin x = - 1 \Leftrightarrow x = - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}.\end{array}\)
3. Phương trình \({\rm{cosx}} = m\)
Phương trình \({\rm{cosx}} = m\)có nghiệm khi và chỉ khi \(\left| m \right| \le 1\).
Khi \(\left| m \right| \le 1\)sẽ tồn tại duy nhất \(\alpha \in \left[ {0;\pi } \right]\) thoả mãn \({\rm{cos}}\alpha = m\). Khi đó:
\({\rm{cosx}} = m \Leftrightarrow {\rm{cosx}} = {\rm{cos}}\alpha \) \( \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
* Chú ý:
a, Nếu số đo của góc \(\alpha \)được cho bằng đơn vị độ thì \(\cos x = \cos {\alpha ^o} \Leftrightarrow \left[ \begin{array}{l}x = {\alpha ^o} + k{360^o}\\x = - {\alpha ^o} + k{360^o}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
b, Một số trường hợp đặc biệt
\(\begin{array}{l}{\rm{cos}}x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}.\\{\rm{cos}}x = 1 \Leftrightarrow x = k2\pi ,k \in \mathbb{Z}.\\{\rm{cos}}x = - 1 \Leftrightarrow x = \pi + k2\pi ,k \in \mathbb{Z}.\end{array}\)
4. Phương trình \(\tan x = m\)
Phương trình \(\tan x = m\)có nghiệm với mọi m.
Với mọi \(m \in \mathbb{R}\), tồn tại duy nhất \(\alpha \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) thoả mãn \(\tan \alpha = m\). Khi đó:
\(\tan {\rm{x}} = m \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi ,k \in \mathbb{Z}.\)
*Chú ý: Nếu số đo của góc \(\alpha \)được cho bằng đơn vị độ thì
\(\tan x = \tan {\alpha ^o} \Leftrightarrow x = {\alpha ^o} + k{180^o},k \in \mathbb{Z}.\)
5. Phương trình \(\cot x = m\)
Phương trình \(\cot x = m\)có nghiệm với mọi m.
Với mọi \(m \in \mathbb{R}\), tồn tại duy nhất \(\alpha \in \left( {0;\pi } \right)\) thoả mãn \(\cot \alpha = m\). Khi đó:
\(\cot {\rm{x}} = m \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi ,k \in \mathbb{Z}.\)
*Chú ý: Nếu số đo của góc \(\alpha \)được cho bằng đơn vị độ thì
\(\cot x = \cot {\alpha ^o} \Leftrightarrow x = {\alpha ^o} + k{180^o},k \in \mathbb{Z}.\)
6. Sử dụng máy tính cầm tay tìm góc khi biết giá trị lượng giác của nó
Bước 1. Chọn đơn vị đo góc (độ hoặc radian).
Muốn tìm số đo độ, ta ấn: SHIFT \( \to \)MODE \( \to \)3 (CASIO FX 570VN).
Muốn tìm số đo radian, ta ấn: SHIFT \( \to \)MODE \( \to \)4 (CASIO FX 570VN).
Bước 2. Tìm số đo góc.
Khi biết SIN, COS, TANG của góc \(\alpha \)ta cần tìm bằng m, ta lần lượt ấn các phím SHIFT và một trong các phím SIN, COS, TANG rồi nhập giá trị lượng giác m và cuối cùng ấn phím “BẰNG =”. Lúc này trên màn hình cho kết quả là số đo của góc \(\alpha \)
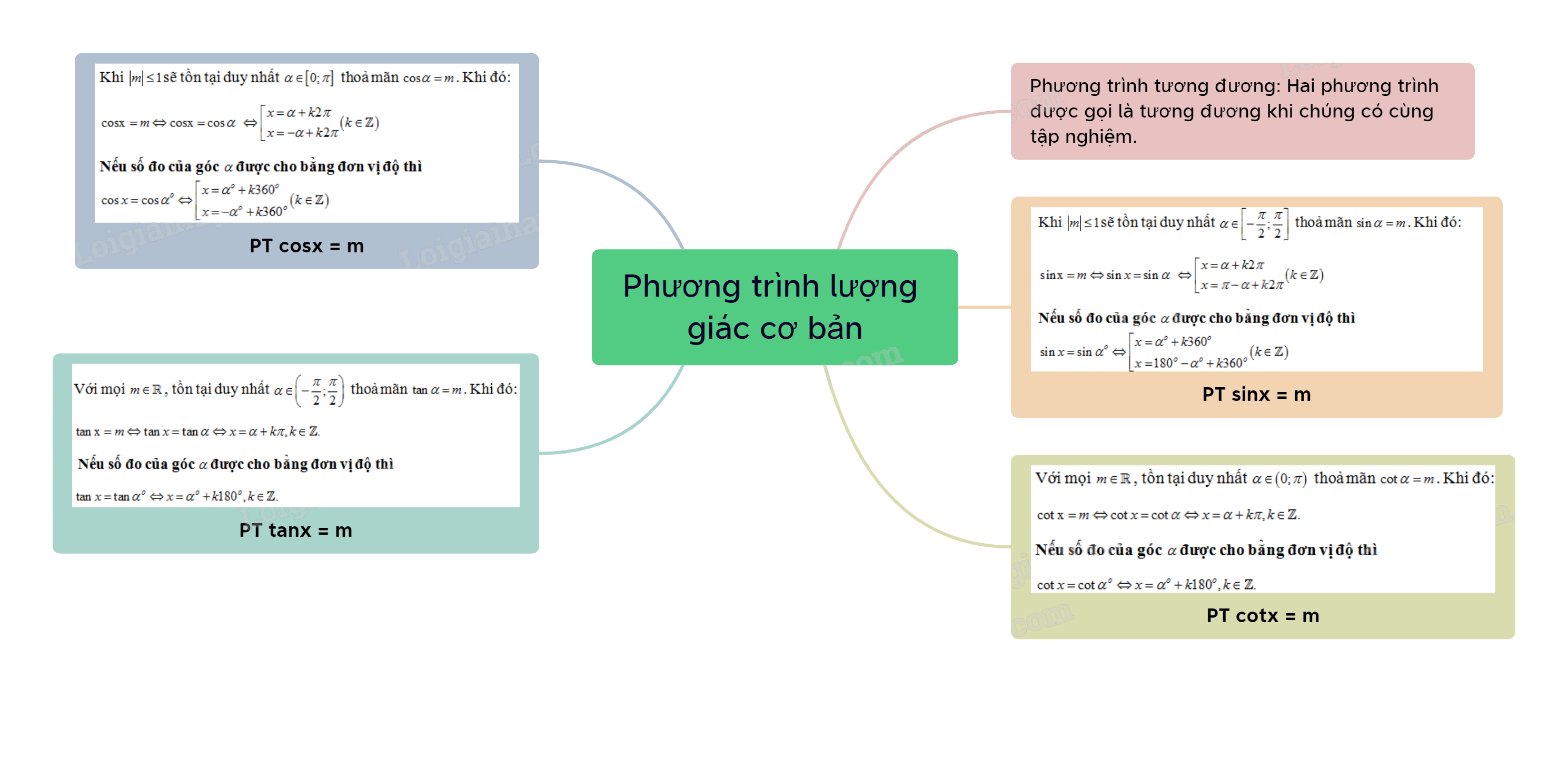
Phương trình lượng giác là phương trình có chứa ẩn số trong biểu thức lượng giác. Giải phương trình lượng giác là tìm các giá trị của ẩn số thỏa mãn phương trình đó. Trong chương trình Toán 11 Kết nối tri thức, chúng ta sẽ tập trung vào các phương trình lượng giác cơ bản, bao gồm:
Phương trình sin(x) = a có nghiệm khi và chỉ khi -1 ≤ a ≤ 1. Khi đó:
Phương trình cos(x) = a có nghiệm khi và chỉ khi -1 ≤ a ≤ 1. Khi đó:
Phương trình tan(x) = a có nghiệm với mọi a ∈ R. Khi đó:
x = arctan(a) + kπ, k ∈ Z
Phương trình cot(x) = a có nghiệm với mọi a ∈ R. Khi đó:
x = arccot(a) + kπ, k ∈ Z
Trong quá trình học và ôn tập, bạn sẽ gặp nhiều dạng bài tập khác nhau liên quan đến phương trình lượng giác cơ bản. Một số dạng bài tập thường gặp bao gồm:
Khi giải phương trình lượng giác, bạn cần lưu ý một số điều sau:
Ví dụ 1: Giải phương trình sin(x) = 1/2
Giải:
Ta có: x = arcsin(1/2) + k2π = π/6 + k2π hoặc x = π - arcsin(1/2) + k2π = 5π/6 + k2π, k ∈ Z
Ví dụ 2: Giải phương trình cos(x) = -√2/2
Giải:
Ta có: x = arccos(-√2/2) + k2π = 3π/4 + k2π hoặc x = -arccos(-√2/2) + k2π = -3π/4 + k2π, k ∈ Z
Lý thuyết Phương trình lượng giác cơ bản là một phần quan trọng của chương trình Toán 11 Kết nối tri thức. Việc nắm vững lý thuyết và phương pháp giải các phương trình lượng giác cơ bản sẽ giúp bạn tự tin hơn khi giải quyết các bài toán liên quan đến lượng giác. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.