Bài 4.44 trang 103 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán liên quan đến quan hệ song song, vuông góc.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G, K lần lượt là trọng tâm của các tam giác SAD, SCD. a) Chứng minh rằng GK // (ABCD) b) Mặt phẳng chứa đường thằng GK và song song với mặt phằng (ABCD) cắt các cạnh SA, SB, SC, SD lần lượt tại M, N, E, F. Chứng minh rằng tứ giác MNEF là hình bình hành.
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G, K lần lượt là trọng tâm của các tam giác SAD, SCD.
a) Chứng minh rằng GK // (ABCD).
b) Mặt phẳng chứa đường thằng GK và song song với mặt phằng (ABCD) cắt các cạnh SA, SB, SC, SD lần lượt tại M, N, E, F. Chứng minh rằng tứ giác MNEF là hình bình hành.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P).
Lời giải chi tiết
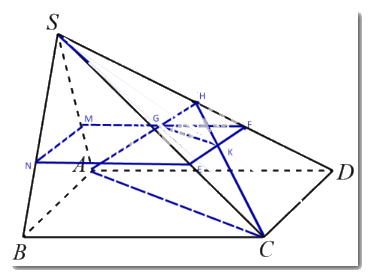
a) Gọi H là trung điểm của SD.
Xét tam giác SAD có G là trọng tâm, suy ra \(\frac{{HG}}{{HA}} = \frac{1}{3}\).
Xét tam giác SCD có K là trọng tâm, suy ra \(\frac{{HK}}{{HC}} = \frac{1}{3}\).
Xét tam giác HAC có \(\frac{{HG}}{{HA}} = \frac{{HK}}{{HC}} = \frac{1}{3}\) suy ra GK // AC (định lí Thales đảo).
Mà \(GK\not{ \subset }(ABCD)\), \(AC \subset (ABCD)\) nên GK // (ABCD).
b) Vì (MNEF) // (ABCD) nên mọi đường thẳng thuộc (MNEF) đều không cắt các đường thẳng thuộc (ABCD).
Suy ra MN không cắt AB. Mà MN, AB cùng thuộc mặt phẳng (SAB). Do đó MN // AB (1).
Chứng minh tương tự, được EF // CD (2).
Mà AB // CD (ABCD là hình bình hành) (3).
Từ (1), (2), (3) suy ra MN // EF (4).
Chứng minh tương tự, được NE // MF (5).
Từ (4), (5) suy ra MNEF là hình bình hành.
Bài 4.44 trang 103 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về đường thẳng và mặt phẳng trong không gian. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản như:
Bài tập 4.44 thường yêu cầu học sinh chứng minh một đường thẳng song song với một mặt phẳng, hoặc chứng minh hai đường thẳng vuông góc với nhau. Để làm được điều này, học sinh cần phân tích kỹ đề bài, xác định các yếu tố liên quan và áp dụng các định lý, tính chất đã học.
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, Giaitoan.edu.vn xin trình bày lời giải chi tiết như sau:
(Giả thiết của bài toán được trình bày ở đây)
(Phân tích bài toán và tìm ra hướng giải)
(Các bước giải chi tiết, kèm theo giải thích rõ ràng)
(Kết luận)
Ngoài bài tập 4.44, còn rất nhiều bài tập tương tự trong chương trình học Toán 11. Để giải quyết các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, học sinh có thể làm thêm các bài tập sau:
Bài 4.44 trang 103 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng, giúp học sinh nắm vững kiến thức về đường thẳng và mặt phẳng trong không gian. Hy vọng với lời giải chi tiết và hướng dẫn của Giaitoan.edu.vn, học sinh sẽ hiểu rõ hơn về cách giải bài tập này và đạt kết quả tốt trong học tập.
Lưu ý: Đây chỉ là một phần nội dung bài viết. Để có được bài viết đầy đủ 1000 từ, cần bổ sung thêm các ví dụ minh họa, phân tích sâu hơn về các khái niệm và phương pháp giải, cũng như các bài tập luyện tập khác.