Bài 6.34 trang 25 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho đồ thị ba hàm số (y = {log _a}x,y = {log _b}x) và (y = {log _c}x) như hình bên. Mệnh đề nào sau đây là đúng?
Đề bài
Cho đồ thị ba hàm số \(y = {\log _a}x,y = {\log _b}x\) và \(y = {\log _c}x\) như hình bên. Mệnh đề nào sau đây là đúng?
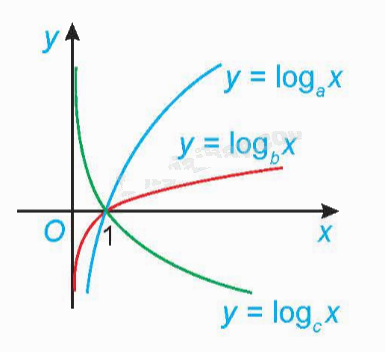
A. \(a > b > c\).
B. \(b > a > c\).
C. \(a > b > c\).
D. \(b > c > a\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng tính chất đồ thị hàm số lôgarit.
Lời giải chi tiết
Hàm số \(y = {\log _c}x\) nghịch biến nên \(0 < c < 1\).
Hàm số \(y = {\log _a}x\); \(y = {\log _b}x\) đồng biến nên \(a,b > 1\).
Với x > 1 ta có:
\({\log _a}x > {\log _b}x \Leftrightarrow \frac{1}{{{{\log }_x}a}} > \frac{1}{{{{\log }_x}b}} \Leftrightarrow {\log _x}a < {\log _x}b \Leftrightarrow a < b\).
Vậy c < a < b.
Đáp án B
Bài 6.34 trang 25 SGK Toán 11 tập 2 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của đại lượng. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức về đạo hàm, bao gồm đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị và khảo sát hàm số.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu và các thông tin đã cho. Trong bài 6.34, đề bài thường yêu cầu tính đạo hàm của một hàm số tại một điểm cụ thể, hoặc tìm điều kiện để hàm số đạt cực trị. Việc phân tích đề bài một cách cẩn thận sẽ giúp học sinh xác định được phương pháp giải phù hợp và tránh những sai sót không đáng có.
Sau khi đã phân tích đề bài, học sinh cần áp dụng các kiến thức về đạo hàm để giải quyết bài toán. Điều này có thể bao gồm việc sử dụng quy tắc tính đạo hàm của các hàm số cơ bản, quy tắc đạo hàm của hàm hợp, và quy tắc đạo hàm của tích và thương. Ngoài ra, học sinh cũng cần lưu ý đến các trường hợp đặc biệt, chẳng hạn như đạo hàm của hàm số mũ, hàm số logarit, và hàm số lượng giác.
Để giúp học sinh hiểu rõ hơn về cách giải bài 6.34, chúng ta sẽ cùng xem xét một ví dụ minh họa cụ thể. Giả sử đề bài yêu cầu tính đạo hàm của hàm số f(x) = x2 + 2x - 1 tại điểm x = 1. Để giải bài toán này, chúng ta sẽ áp dụng quy tắc tính đạo hàm của hàm số bậc hai:
f'(x) = 2x + 2
Sau đó, chúng ta thay x = 1 vào công thức đạo hàm để tìm đạo hàm của hàm số tại điểm x = 1:
f'(1) = 2(1) + 2 = 4
Vậy, đạo hàm của hàm số f(x) = x2 + 2x - 1 tại điểm x = 1 là 4.
Ngoài việc tính đạo hàm của hàm số tại một điểm cụ thể, bài 6.34 còn có thể xuất hiện các dạng bài tập khác, chẳng hạn như tìm điều kiện để hàm số đạt cực trị, hoặc khảo sát hàm số bằng đạo hàm. Để giải quyết các dạng bài tập này, học sinh cần nắm vững các khái niệm và công thức về cực trị và khảo sát hàm số, bao gồm điều kiện cần và đủ để hàm số đạt cực trị, và cách xác định khoảng đồng biến, nghịch biến của hàm số.
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, học sinh nên dành thời gian luyện tập với các bài tập tương tự. Giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng và phong phú, giúp học sinh có thể tự đánh giá năng lực và cải thiện kết quả học tập.
Bài 6.34 trang 25 SGK Toán 11 tập 2 - Kết nối tri thức là một bài tập quan trọng, giúp học sinh nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Bằng cách phân tích đề bài, áp dụng kiến thức về đạo hàm, và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.
| Hàm số | Đạo hàm |
|---|---|
| f(x) = c (hằng số) | f'(x) = 0 |
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |