Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 81 và 82 sách giáo khoa Toán 11 tập 2, chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Một vật di chuyển trên một đường thẳng (H.9.2).
Video hướng dẫn giải
Một vật di chuyển trên một đường thẳng (H.9.2). Quãng đường s của chuyển động là một hàm số của thời gian t, s = s(t) (được gọi là phương trình của chuyển động).
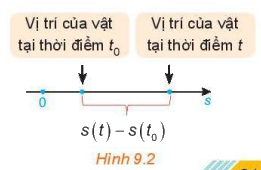
a) Tính vận tốc trung bình của vật trong khoảng thời gian từ t0 đến t.
b Giới hạn \(\mathop {\lim }\limits_{t \to {t_0}} \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}}\) cho ta biết điều gì?
Phương pháp giải:
Vận tốc trung bình bằng tổng quãng đường đi được chia cho thời gian chuyển động
Lời giải chi tiết:
a) Vận tốc trung bình của vật trong khoảng thời gian từ t0 đến t là \({v_{tb}} = \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}}\)
b) Khi t càng gần t0, tức là \(\left| {t - {t_0}} \right|\) càng nhỏ thì vận tốc trung bình càng thể hiện được chính xác hơn mức độ nhanh chậm của chuyển động tại thời điểm t0.
Video hướng dẫn giải
Điện lượng Q truyền trong dây dẫn là một hàm số của thời gian t, có dạng Q = Q(t).
a) Tính cường độ trung bình của dòng điện trong khoảng thời gian từ t0 đến t.
b) Giới hạn \(\mathop {\lim }\limits_{t \to {t_0}} \frac{{Q\left( t \right) - Q\left( {{t_0}} \right)}}{{t - {t_0}}}\) cho ta biết điều gì?
Phương pháp giải:
Cường độ trung bình của dòng điện là thương số giữa điện lượng chuyển qua bề mặt trong khoảng thời gian đó và khoảng thời gian đang xét.
Lời giải chi tiết:
a) Cường độ trung bình của dòng điện trong khoảng thời gian từ t0 đến t là \({I_{tb}} = \frac{{Q\left( t \right) - Q\left( {{t_0}} \right)}}{{t - {t_0}}}\)
b) Khi t càng gần t0, tức là \(\left| {t - {t_0}} \right|\) càng nhỏ thì cường độ trung bình càng thể hiện được chính xác hơn cường độ dòng điện tại thời điểm t0.
Mục 1 của chương trình Toán 11 tập 2, Kết nối tri thức, tập trung vào việc ôn tập và mở rộng kiến thức về đạo hàm. Các bài tập trang 81 và 82 SGK Toán 11 tập 2 yêu cầu học sinh vận dụng các công thức và quy tắc đạo hàm đã học để giải quyết các bài toán thực tế. Việc nắm vững kiến thức nền tảng và kỹ năng giải toán là vô cùng quan trọng để hoàn thành tốt các bài tập này.
Bài tập này yêu cầu học sinh tính đạo hàm của các hàm số đơn thức, đa thức, và các hàm số phức tạp hơn. Để giải bài tập này, học sinh cần nắm vững các quy tắc đạo hàm cơ bản như quy tắc đạo hàm của tổng, hiệu, tích, thương, và quy tắc đạo hàm của hàm hợp.
Bài tập này yêu cầu học sinh tìm đạo hàm của hàm số tại một điểm cụ thể. Để giải bài tập này, học sinh cần tính đạo hàm của hàm số y = f(x) và sau đó thay x = x0 vào đạo hàm để tìm giá trị của đạo hàm tại điểm đó.
Bài tập này yêu cầu học sinh áp dụng đạo hàm để giải các bài toán thực tế như tìm vận tốc, gia tốc, hoặc tối ưu hóa các đại lượng. Để giải bài tập này, học sinh cần hiểu rõ ý nghĩa vật lý của đạo hàm và biết cách thiết lập mô hình toán học phù hợp.
Dưới đây là hướng dẫn giải chi tiết cho từng bài tập trong mục 1 trang 81 và 82 SGK Toán 11 tập 2, Kết nối tri thức:
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 81 và 82 SGK Toán 11 tập 2, Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao!