Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 Kết nối tri thức. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3, trang 10, 11, 12 và 13 của sách giáo khoa.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập phức tạp. Vì vậy, giaitoan.edu.vn luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính R = 1. Chọn điểm gốc của đường tròn là giao điểm A(1;0)
Video hướng dẫn giải
Trong mặt phẳng tọa độ vẽ đường tròn tâm O bán kính R = 1. Chọn điểm gốc của đường tròn là giao điểm của đường tròn với trục . Ta quy ước chiều dương của đường tròn là chiều ngược chiều quay của kim đồng hồ và chiều âm là chiều quay của kim đồng hồ.
a) Xác định điểm trên đường tròn sao cho sđ\((OA,OM) = \frac{{5\pi }}{4}\)
b) Xác định điểm trên đường tròn sao cho sđ\((OA,ON) = - \frac{{7\pi }}{4}\)
Phương pháp giải:
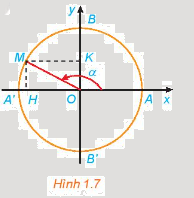
Đường tròn lượng giác có tâm tại gốc tọa độ, bán kính bằng 1, lấy điểm A(1;0) là gốc của đường tròn.
Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là điểm M trên đường tròn lượng giác sao cho sđ\((OA,OM) = \alpha \)
Lời giải chi tiết:
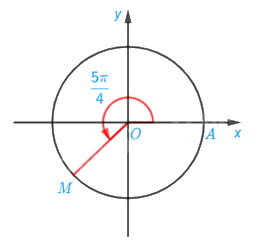
a) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng \(\frac{{5\pi }}{4}\) được xác định trong hình.
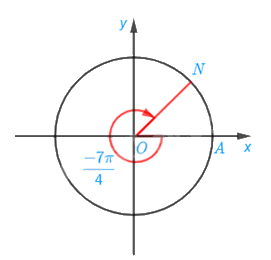
b) Điểm N trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng\( - \frac{{7\pi }}{4}\)được xác định là điểm chính giữa cung BA.
Video hướng dẫn giải
Xác định điểm M và N trên đường tròn lượng giác lần lượt biểu diễn các góc lượng giác có số đo bằng \( - \frac{{15\pi }}{4}\)và \({420^ \circ }\)
Phương pháp giải:
Đường tròn lượng giác có tâm tại gốc tọa độ, bán kính bằng 1, lấy điểm A(1;0) là gốc của đường tròn.
Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là điểm M trên đường tròn lượng giác sao cho sđ\((OA,OM) = \alpha \)
Lời giải chi tiết:
Điểm biểu diễn góc lượng giác có số đo bằng \( - \frac{{15\pi }}{4} = - \frac{{7\pi }}{4} + ( - 1).2\pi \) được xác định là điểm M.

Ta có \(\frac{{420}}{{360}} = 1+ \frac{1}{6}\) Ta chia đường tròn thành 6 phần bằng nhau. Khi đó điểm N là điểm biểu diễn bởi góc có số đo \({420^ \circ }\)

Video hướng dẫn giải
Nhắc lại khái niệm các giá trị lượng giác \(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) của góc \(\alpha \)\(({0^ \circ } \le \alpha \le {180^ \circ })\) đã học ở lớp 10
Phương pháp giải:
Dựa vào kiến thức đã học để nhắc lại.
Lời giải chi tiết:

+) Nửa đường tròn đơn vị: nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành (H.3.2).
+) Với mỗi góc \(\alpha ({0^o} \le \alpha \le {180^o})\)có duy nhất điểm \(M({x_0};{y_0})\) trên nửa đường tròn đơn vị nói trên để \(\widehat {xOM} = \alpha .\) Khi đó:
\(\sin \alpha = {y_0}\) là tung độ của M
\(\cos \alpha = {x_0}\) là hoành độ của M
\(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha \ne {90^o})\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha \ne {0^o},\alpha \ne {180^o})\)
Video hướng dẫn giải
Cho góc lượng giác có số đo bằng \(\frac{{5\pi }}{6}\)
a) Xác định điểm M trên đường tròn lượng giác biểu diễn góc lượng giác đã cho.
b) Tính các giá trị lượng giác của góc lượng giác đã cho.
Phương pháp giải:
Áp dụng \(\sin \alpha = y\) ; \(\cos \alpha = x\) ; \(\tan \alpha =\frac{y}{x}\) ; \(\cot \alpha =\frac{x}{y}\)
Lời giải chi tiết:
a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo \(\frac{{5\pi }}{6}\)

b) Ta có:
\(\sin \left( {\frac{{5\pi }}{6}} \right) = \frac{1}{2};\cos \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{2};\tan \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{3};\cot \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - 3}}{{\sqrt 3 }}\)
Video hướng dẫn giải
Sử dụng máy tính cầm tay để:
a) Tính: \(\cos \frac{{3\pi }}{7};\tan ( - {37^ \circ }25')\)
b) Đổi \({179^ \circ }23'30''\) sang rađian;
c) Đổi \(\frac{{7\pi }}{9}\)(rad) sang độ.
Phương pháp giải:
Sử dụng máy tính cầm tay
Lời giải chi tiết:
a) \(\cos \frac{{3\pi }}{7} = 0,22252\);
\(\tan ( - {37^ \circ }25') = -0,765018\)
b) Đổi 179°23'30" sang rađian ta thực hiện bấm phím lần lượt như sau:

Màn hình hiện 3,130975234
Vậy 179°23'30" ≈ 3,130975234 (rad).
c) \(\frac{{7\pi }}{9}\) (rad) = \(140^ \circ \)".
Mục 3 trong SGK Toán 11 tập 1 Kết nối tri thức tập trung vào các kiến thức về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng, không chỉ trong chương trình Toán học phổ thông mà còn là bước đệm cho các kiến thức nâng cao ở bậc đại học.
Để hiểu rõ về giới hạn của hàm số, trước tiên chúng ta cần nắm vững định nghĩa. Giới hạn của hàm số f(x) khi x tiến tới a (ký hiệu là lim x→a f(x)) là giá trị mà hàm số f(x) tiến gần tới khi x lấy các giá trị gần a nhưng không bằng a.
Việc tính giới hạn hàm số có thể được thực hiện bằng nhiều phương pháp khác nhau, tùy thuộc vào dạng của hàm số. Một số phương pháp phổ biến bao gồm:
Bài 1 (Trang 10): Tính lim x→2 (x^2 + 3x - 1). Giải: Thay x = 2 vào biểu thức, ta được 2^2 + 3*2 - 1 = 4 + 6 - 1 = 9. Vậy lim x→2 (x^2 + 3x - 1) = 9.
Bài 2 (Trang 11): Tính lim x→-1 (x^3 - 2x + 1). Giải: Thay x = -1 vào biểu thức, ta được (-1)^3 - 2*(-1) + 1 = -1 + 2 + 1 = 2. Vậy lim x→-1 (x^3 - 2x + 1) = 2.
Bài 3 (Trang 12): Tính lim x→0 (sin x / x). Giải: Đây là một giới hạn lượng giác cơ bản. Sử dụng định lý giới hạn đặc biệt, ta có lim x→0 (sin x / x) = 1.
Bài 4 (Trang 13): Tính lim x→1 (x^2 - 1) / (x - 1). Giải: Ta phân tích tử thành nhân tử: x^2 - 1 = (x - 1)(x + 1). Vậy lim x→1 (x^2 - 1) / (x - 1) = lim x→1 (x + 1) = 1 + 1 = 2.
Khi giải bài tập về giới hạn, các em cần lưu ý một số điểm sau:
Khái niệm giới hạn không chỉ có ý nghĩa trong Toán học mà còn có nhiều ứng dụng trong thực tế, chẳng hạn như:
Hy vọng rằng với những giải thích chi tiết và ví dụ minh họa trên, các em đã hiểu rõ hơn về cách giải các bài tập trong mục 3 trang 10,11,12,13 SGK Toán 11 tập 1 Kết nối tri thức. Chúc các em học tập tốt!