Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 2 trang 97 và 98 sách giáo khoa Toán 11 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Quan sát Hình 4.56a và trả lời các câu hỏi sau: a) Hình chiếu O’ của điểm O có nằm trên đoạn A’C’ hay không? b) Hình chiếu của hai song cửa AB và CD như thế nào với nhau? c) Hình chiếu O’ của điểm O có phải là trung điểm của đoạn A’C’ hay
Video hướng dẫn giải
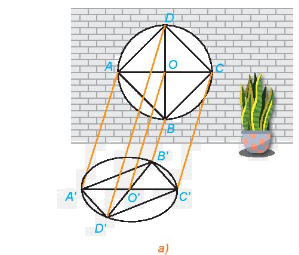
Quan sát Hình 4.56a và trả lời các câu hỏi sau:
a) Hình chiếu O’ của điểm O có nằm trên đoạn A’C’ hay không?
b) Hình chiếu của hai song cửa AB và CD như thế nào với nhau?
c) Hình chiếu O’ của điểm O có phải là trung điểm của đoạn A’C’ hay không?
Phương pháp giải:
Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.
Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
Lời giải chi tiết:
a) Hình chiếu O’ của điểm O nằm trên đoạn A’C’.
b) Hình chiếu song song của AB và CD song song với AB và CD.
c) Hình chiếu O’ của điểm O là trung điểm của đoạn A’C’.
Video hướng dẫn giải
Chứng minh rằng hình chiếu song song của một hình thang là một hình thang (H.4.61).

Phương pháp giải:
Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.
Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
Lời giải chi tiết:
Vì ABCD là hình thang nên AB // CD, do đó hình chiếu của AB là A'B' song song với hình chiếu của CD là C'D'.
Tứ giác A'B'C'D' có A'B' // C'D' nên nó là hình thang.
Video hướng dẫn giải
Một phép chiếu song song biến tam giác ABC thành tam giác A’B’C’, biến M thành M’. Chứng minh rằng phép chiếu đó biến đường trung bình của tam giác ABC thành đường trung bình của tam giác A’B’C’.

Phương pháp giải:
Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.
Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
Lời giải chi tiết:
Gọi N là trung điểm của AC. Khi đó MN là đường trung bình của tam giác ABC.
Vì M là trung điểm của BC nên B, M, C thẳng hàng theo thứ tự đó và \(\frac{{BM}}{{MC}} = 1\).
Do vậy, B’, M’, C’ thẳng hàng theo thứ tự đó và \(\frac{{B'M'}}{{M'C'}} = 1\).
Tức M’ là trung điểm của B’C’.
Tương tự, N’ là trung điểm của A’C’.
Vậy M’N’ là đường trung bình của tam giác A’B’C’.
Mục 2 của chương trình Toán 11 tập 1 Kết nối tri thức tập trung vào các kiến thức về phép biến hình. Cụ thể, các em sẽ được làm quen với các khái niệm như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các kiến thức này là nền tảng quan trọng để giải quyết các bài toán hình học trong chương trình học.
Phép tịnh tiến là một phép biến hình quan trọng trong hình học. Phép tịnh tiến biến mỗi điểm M thành điểm M' sao cho vector MM' = v (với v là vector tịnh tiến). Để giải các bài toán liên quan đến phép tịnh tiến, các em cần nắm vững các tính chất của phép tịnh tiến như bảo toàn khoảng cách, bảo toàn góc và bảo toàn thứ tự các điểm.
Phép quay là một phép biến hình biến mỗi điểm M thành điểm M' sao cho khoảng cách từ M đến tâm quay O bằng khoảng cách từ M' đến tâm quay O và góc MOM' bằng một góc cho trước. Các em cần chú ý đến việc xác định tâm quay, góc quay và chiều quay để giải quyết các bài toán liên quan đến phép quay.
Phép đối xứng trục là một phép biến hình biến mỗi điểm M thành điểm M' sao cho M' nằm trên đường thẳng d (trục đối xứng) và đường thẳng d là đường trung trực của đoạn thẳng MM'. Để giải các bài toán liên quan đến phép đối xứng trục, các em cần xác định đúng trục đối xứng và tìm điểm đối xứng của mỗi điểm.
Phép đối xứng tâm là một phép biến hình biến mỗi điểm M thành điểm M' sao cho M' nằm trên đường thẳng đi qua M và tâm đối xứng O, và O là trung điểm của đoạn thẳng MM'. Các em cần chú ý đến việc xác định tâm đối xứng để giải quyết các bài toán liên quan đến phép đối xứng tâm.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 2 trang 97 và 98 sách giáo khoa Toán 11 tập 1 chương trình Kết nối tri thức:
Ví dụ minh họa:
Giả sử chúng ta có điểm A(1; 2) và vector tịnh tiến v = (3; -1). Hãy tìm tọa độ điểm A' là ảnh của điểm A qua phép tịnh tiến theo vector v.
Lời giải:
Tọa độ điểm A' được tính như sau:
x' = x + vx = 1 + 3 = 4
y' = y + vy = 2 + (-1) = 1
Vậy, tọa độ điểm A' là (4; 1).
Hy vọng với những kiến thức và lời giải chi tiết trên, các em sẽ tự tin hơn trong việc giải các bài tập về phép biến hình. Chúc các em học tập tốt!