Bài 7.25 thuộc chương trình Toán 11 tập 2, sách Kết nối tri thức, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm, điểm cực trị và các tính chất của hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 7.25, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
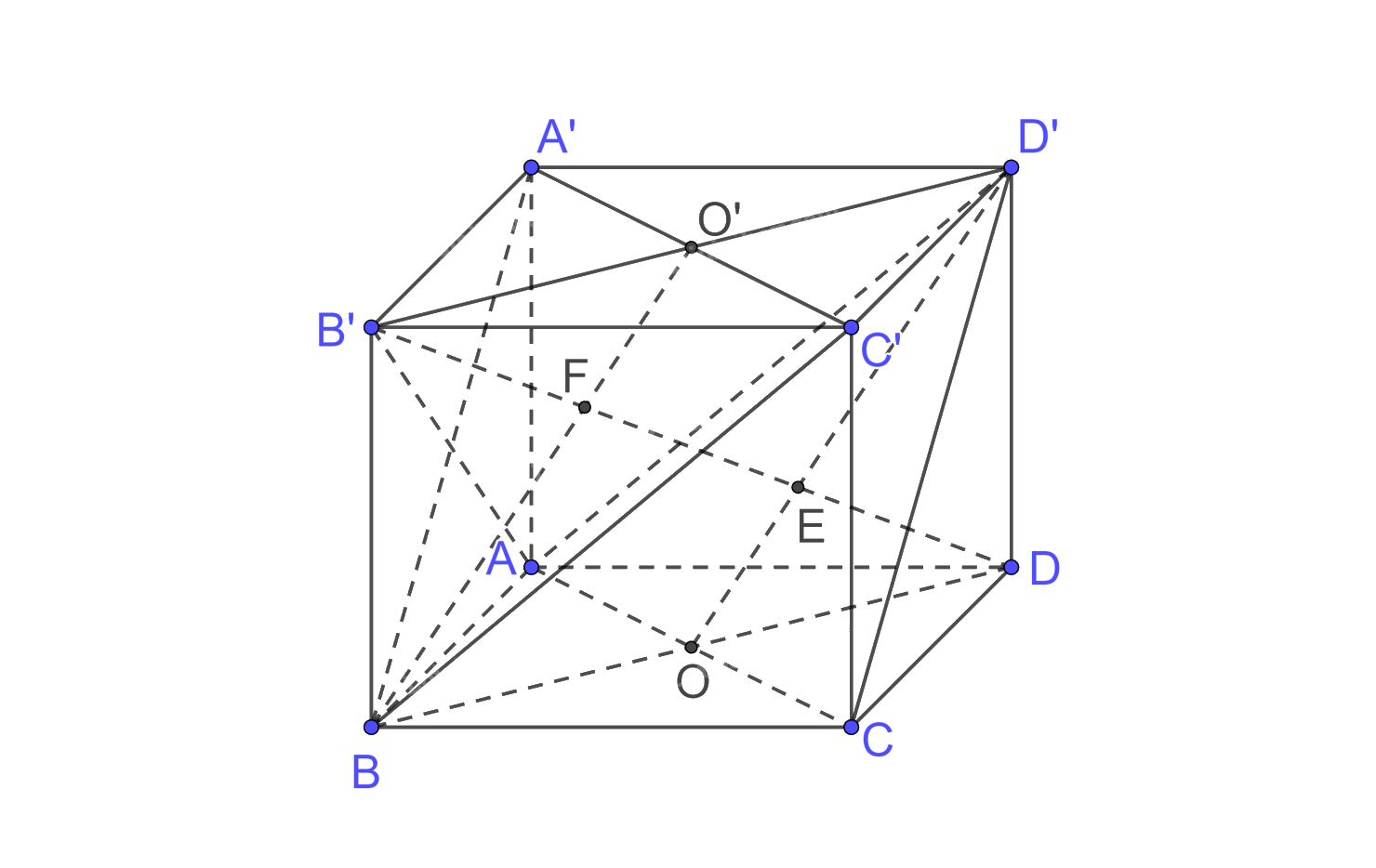
Cho hình lập phương ABCD.A'B'C'D' có cạnh a.
Đề bài
Cho hình lập phương ABCD.A'B'C'D' có cạnh a.
a) Chứng minh rằng hai mặt phẳng (D'AC) và (BC'A') song song với nhau và DB' vuông góc với hai mặt phẳng đó.
b) Xác định các giao điểm E, F của DB' với (D'AC),(BC'A'). Tính d((D'AC), (BC'A')).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Hai mặt phẳng song song nếu 2 đường thẳng cắt nhau trong mặt phẳng này lần lượt song song với 2 đường thẳng cắt nhau trong mặt phẳng kia.
- Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia.
Lời giải chi tiết
a) AC // A’C’, D’C // A’B \( \Rightarrow \) (D'AC) // (BC'A')
Ta có \(AC \bot BD,AC \bot BB' \Rightarrow AC \bot \left( {BDB'} \right);B'D \subset \left( {BDB'} \right) \Rightarrow AC \bot B'D\)
Mà AC // A’C’ \( \Rightarrow \) \(B'D \bot A'C'\)
Ta có \(AB' \bot A'B,AD \bot A'B \Rightarrow A'B \bot \left( {AB'D} \right);B'D \subset \left( {AB'D} \right) \Rightarrow A'B \bot B'D\)
Mà A’B // D’C \( \Rightarrow \) \(B'D \bot D'C\)
Ta có \(B'D \bot AC,B'D \bot D'C \Rightarrow B'D \bot \left( {D'AC} \right)\)
\(B'D \bot A'C',B'D \bot A'B \Rightarrow B'D \bot \left( {BA'C'} \right)\)
b) Gọi \(AC \cap BD = \left\{ O \right\},A'C' \cap B'D' = \left\{ {O'} \right\}\)
Trong (BB’D’D) nối \(D'O \cap B'D = \left\{ E \right\},BO' \cap B'D = \left\{ F \right\}\)
Vì (D'AC) // (BC'A') nên d((D'AC), (BC'A')) = d(E, (BC'A')) = EF do \(B'D \bot \left( {BA'C'} \right)\)
\(\left. \begin{array}{l}B'D \bot BO'\left( {B'D \bot \left( {BA'C'} \right)} \right)\\B'D \bot OD'\left( {B'D \bot \left( {D'AC} \right)} \right)\end{array} \right\} \Rightarrow BO'//OD'\)
Áp dụng định lí Talet có \(\frac{{DE}}{{EF}} = \frac{{DO}}{{BO}} = 1 \Rightarrow DE = EF\) và \(\frac{{B'F}}{{EF}} = \frac{{B'O'}}{{O'D'}} = 1 \Rightarrow B'F = EF\)
\( \Rightarrow EF = \frac{{B'D}}{3}\)
Xét tam giác ABD vuông tại A có \(BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
Xét tam giác BB’D vuông tại B có \(B'D = \sqrt {B{{B'}^2} + B{D^2}} = \sqrt {{a^2} + {{\left( {a\sqrt 2 } \right)}^2}} = a\sqrt 3 \)
\( \Rightarrow EF = \frac{{a\sqrt 3 }}{3}\)
Vậy \(d\left( {\left( {D'AC} \right),{\rm{ }}\left( {BC'A'} \right)} \right) = \frac{{a\sqrt 3 }}{3}\)
Bài 7.25 SGK Toán 11 tập 2 Kết nối tri thức yêu cầu học sinh giải một bài toán thực tế liên quan đến việc tối ưu hóa một đại lượng nào đó bằng cách sử dụng đạo hàm. Để giải bài toán này, chúng ta cần thực hiện các bước sau:
Giả sử bài toán yêu cầu tìm kích thước của một hình chữ nhật có diện tích cho trước sao cho chu vi nhỏ nhất. Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là x và y. Diện tích hình chữ nhật là S = xy (không đổi) và chu vi là P = 2(x + y). Chúng ta cần tìm x và y sao cho P nhỏ nhất.
Từ S = xy, ta có y = S/x. Thay vào công thức tính chu vi, ta được P = 2(x + S/x). Đạo hàm P theo x, ta có P' = 2(1 - S/x^2). Giải phương trình P' = 0, ta được x^2 = S, suy ra x = √S (vì x > 0). Khi đó, y = S/√S = √S. Vậy, hình chữ nhật có chu vi nhỏ nhất là hình vuông có cạnh bằng √S.
Các bài tập tương tự Bài 7.25 thường yêu cầu tối ưu hóa các đại lượng như diện tích, thể tích, chi phí, lợi nhuận,... trong các bài toán thực tế. Để giải các bài tập này, cần áp dụng linh hoạt các kiến thức về đạo hàm và ứng dụng của đạo hàm.
Bài 7.25 trang 59 SGK Toán 11 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải các bài toán tối ưu hóa bằng cách sử dụng đạo hàm. Việc nắm vững kiến thức và phương pháp giải bài tập này sẽ giúp các em học sinh tự tin hơn trong việc giải các bài toán tương tự và ứng dụng toán học vào thực tế.