Chào mừng bạn đến với bài học về Lý thuyết Giới hạn của dãy số, một phần quan trọng trong chương trình Toán 11 Kết nối tri thức.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và nâng cao về giới hạn của dãy số, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
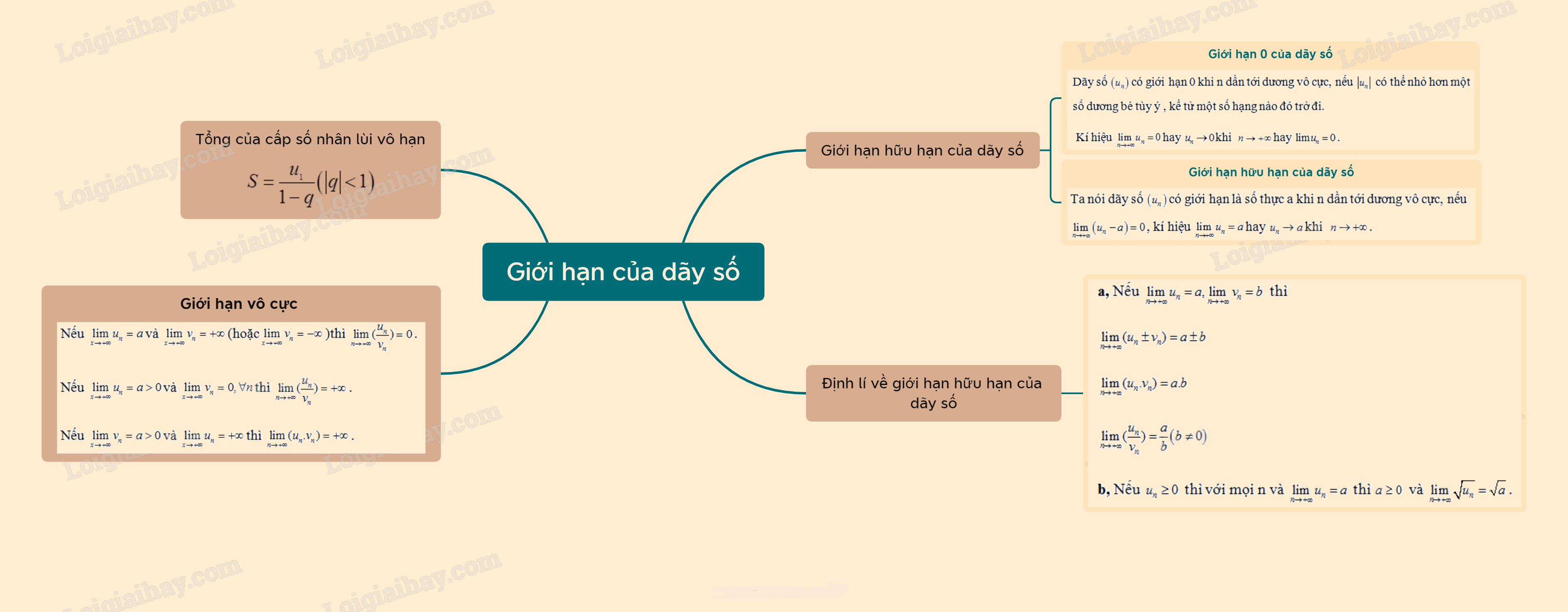
1, Giới hạn hữu hạn của dãy số
1, Giới hạn hữu hạn của dãy số
Ta nói dãy số \(\left( {{u_n}} \right)\) có giới hạn 0 khi n dần tới dương vô cực, nếu \(\left| {{u_n}} \right|\) có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi, kí hiệu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 0\) hay \({u_n} \to 0\) khi \(n \to + \infty \).
Ta nói dãy số \(\left( {{u_n}} \right)\) có giới hạn là số thực a khi n dần tới dương vô cực, nếu \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - a} \right) = 0\), kí hiệu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\) hay \({u_n} \to a\) khi \(n \to + \infty \).
* Chú ý: Nếu \({u_n} = c\) (c là hằng số) thì \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = c\)
2. Định lí về giới hạn hữu hạn của dãy số
a, Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b\) thì
\(\mathop {\lim }\limits_{n \to + \infty } ({u_n} \pm {v_n}) = a \pm b\)
\(\mathop {\lim }\limits_{n \to + \infty } ({u_n}.{v_n}) = a.b\)
\(\mathop {\lim }\limits_{n \to + \infty } (\frac{{{u_n}}}{{{v_n}}}) = \frac{a}{b}\left( {b \ne 0} \right)\)
b, Nếu \({u_n} \ge 0\) thì với mọi n và \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\) thì \(a \ge 0\) và \(\mathop {\lim }\limits_{n \to + \infty } \sqrt {{u_n}} = \sqrt a \).
3. Tổng của cấp số nhân lùi vô hạn
\(S = \frac{{{u_1}}}{{1 - q}}\left( {\left| q \right| < 1} \right)\)
4. Giới hạn vô cực của dãy số
Dãy số \(\left( {{u_n}} \right)\) được gọi là có giới hạn \( + \infty \)khi \(n \to + \infty \)nếu \({u_n}\) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi, kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = + \infty \) hay \({u_n} \to + \infty \) khi \(n \to + \infty \).
Dãy số \(\left( {{u_n}} \right)\) được gọi là có giới hạn \( - \infty \) khi \(n \to + \infty \) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left( { - {u_n}} \right) = + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = - \infty \) hay \({u_n} \to - \infty \) khi \(n \to + \infty \).
*Quy tắc:
Nếu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = a\) và \(\mathop {\lim }\limits_{x \to + \infty } {v_n} = + \infty \)(hoặc\(\mathop {\lim }\limits_{x \to + \infty } {v_n} = - \infty \)) thì \(\mathop {\lim }\limits_{n \to + \infty } (\frac{{{u_n}}}{{{v_n}}}) = 0\).
Nếu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = a > 0\) và \(\mathop {\lim }\limits_{x \to + \infty } {v_n} = 0,\forall n\) thì \(\mathop {\lim }\limits_{n \to + \infty } (\frac{{{u_n}}}{{{v_n}}}) = + \infty \).
Nếu \(\mathop {\lim }\limits_{x \to + \infty } {v_n} = a > 0\) và \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = + \infty \) thì \(\mathop {\lim }\limits_{n \to + \infty } ({u_n}.{v_n}) = + \infty \).
Giới hạn của dãy số là một khái niệm nền tảng trong giải tích, đóng vai trò quan trọng trong việc nghiên cứu sự hội tụ và phân kỳ của dãy số. Hiểu rõ lý thuyết này là bước đệm quan trọng để tiếp cận các khái niệm phức tạp hơn trong toán học.
Một dãy số (un) được gọi là có giới hạn L nếu với mọi ε > 0, tồn tại một số tự nhiên N sao cho với mọi n > N, ta có |un - L| < ε. Ký hiệu: limn→∞ un = L.
Trong đó:
Dãy số có thể có các dạng giới hạn sau:
Các tính chất quan trọng của giới hạn dãy số bao gồm:
Ví dụ 1: Tính giới hạn của dãy số un = 1/n.
limn→∞ (1/n) = 0. Vì khi n tiến tới vô cùng, 1/n tiến tới 0.
Ví dụ 2: Tính giới hạn của dãy số un = n2.
limn→∞ n2 = +∞. Vì khi n tiến tới vô cùng, n2 cũng tiến tới vô cùng.
Khi tính giới hạn của dãy số, cần chú ý đến các trường hợp đặc biệt như dãy số không xác định, dãy số dao động và các tính chất của giới hạn để đảm bảo kết quả chính xác.
Nắm vững lý thuyết giới hạn của dãy số là bước đầu tiên để bạn có thể giải quyết các bài toán phức tạp hơn trong chương trình Toán 11 và các môn học liên quan. Chúc bạn học tập tốt!