Giải Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức

Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức

Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức: Giải pháp học toán hiệu quả

Bài 13 trang 106 SGK Toán 11 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.

Hãy cùng khám phá lời giải Bài 13 trang 106 SGK Toán 11 tập 2 ngay bây giờ!

Cho tứ diện đều ABCD có cạnh bằng (a). Gọi M, N lần lượt là trung điểm của cạnh AC và cạnh AD.

Đề bài

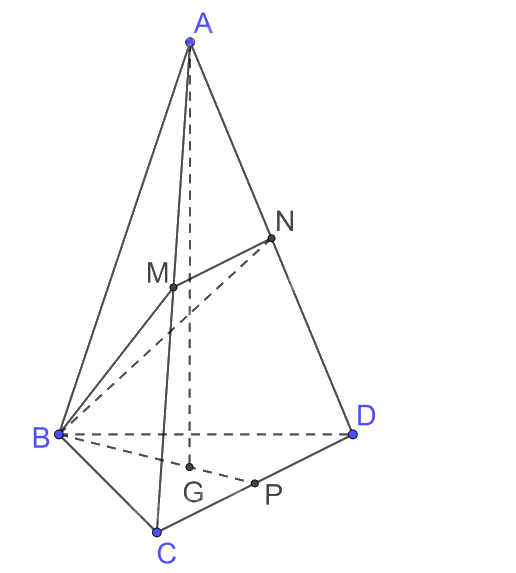
Cho tứ diện đều ABCD có cạnh bằng \(a\). Gọi M, N lần lượt là trung điểm của cạnh AC và cạnh AD. Thể tích khối chóp \(B\).CMND bằng

A. \(\frac{{{a^3}\sqrt 2 }}{{12}}\)

B. \(\frac{{{a^3}\sqrt 2 }}{{16}}\).

C. \(\frac{{{a^3}\sqrt 2 }}{{24}}\).

D. \(\frac{{{a^3}\sqrt 2 }}{8}\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức 1

- Thể tích khối chóp đều cạnh a: \(V = \frac{{\sqrt 2 {a^3}}}{{12}}\)

- Tỉ lệ thể tích: \(\frac{{{V_{S.ABC}}}}{{{V_{S.A'B'C'}}}} = \frac{{SA}}{{SA'}}.\frac{{SB}}{{SB'}}.\frac{{SC}}{{SC'}}\)

Lời giải chi tiết

Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức 2

Thể tích khối chóp đều cạnh a: \(V = \frac{{\sqrt 2 {a^3}}}{{12}}\)

Ta có \(\frac{{{V_{A.BMN}}}}{{{V_{A.BCD}}}} = \frac{{AB}}{{AB}}.\frac{{AM}}{{AC}}.\frac{{AN}}{{AD}} = \frac{1}{2}.\frac{1}{2} = \frac{1}{4}\)

Mà \({V_{A.BCD}} = {V_{A.BMN}} + {V_{B.CMND}}\)

\( \Rightarrow {V_{B.CMND}} = \frac{3}{4}{V_{ABCD}} = \frac{3}{4}.\frac{{\sqrt 2 {a^3}}}{{12}} = \frac{{\sqrt 2 {a^3}}}{{16}}\)

Đáp án B

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức – hành trang không thể thiếu trong chuyên mục Đề thi Toán lớp 11 trên nền tảng soạn toán. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức: Giải chi tiết và hướng dẫn

Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến khảo sát hàm số. Để giải bài tập này một cách hiệu quả, cần nắm vững các bước sau:

Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
Tính đạo hàm cấp một: Sử dụng các quy tắc đạo hàm để tìm đạo hàm f'(x).
Tìm điểm tới hạn: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng không.
Khảo sát tính đơn điệu của hàm số: Xét dấu đạo hàm f'(x) trên các khoảng xác định để xác định khoảng hàm số đồng biến và nghịch biến.
Tìm cực trị của hàm số: Dựa vào dấu của đạo hàm để xác định các điểm cực đại và cực tiểu của hàm số.
Tính đạo hàm cấp hai: Tìm đạo hàm f''(x).
Tìm điểm uốn: Giải phương trình f''(x) = 0 để tìm các điểm uốn của hàm số.
Khảo sát tính lồi lõm của hàm số: Xét dấu đạo hàm f''(x) trên các khoảng xác định để xác định khoảng hàm số lồi và lõm.
Vẽ đồ thị hàm số: Dựa vào các thông tin đã thu thập để vẽ đồ thị hàm số.

Ví dụ minh họa

Giả sử hàm số cần khảo sát là y = x³ - 3x² + 2. Ta thực hiện các bước sau:

Tập xác định: D = ℝ
Đạo hàm cấp một: y' = 3x² - 6x
Điểm tới hạn: 3x² - 6x = 0 => x = 0 hoặc x = 2
Khảo sát tính đơn điệu:
- x < 0: y' > 0 => Hàm số đồng biến
- 0 < x < 2: y' < 0 => Hàm số nghịch biến
- x > 2: y' > 0 => Hàm số đồng biến
Cực trị:
- x = 0: Điểm cực đại, y = 2
- x = 2: Điểm cực tiểu, y = -2
Đạo hàm cấp hai: y'' = 6x - 6
Điểm uốn: 6x - 6 = 0 => x = 1
Khảo sát tính lồi lõm:
- x < 1: y'' < 0 => Hàm số lõm
- x > 1: y'' > 0 => Hàm số lồi

Lưu ý quan trọng

Khi giải Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức, cần chú ý đến việc kiểm tra lại các bước tính toán và đảm bảo rằng các kết quả thu được là chính xác. Ngoài ra, việc vẽ đồ thị hàm số cũng rất quan trọng để hiểu rõ hơn về tính chất của hàm số.

Bài tập tương tự

Để củng cố kiến thức, bạn có thể luyện tập thêm các bài tập tương tự trong SGK Toán 11 tập 2 - Kết nối tri thức hoặc các đề thi thử Toán 11.

Kết luận

Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán và hiểu sâu hơn về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và hướng dẫn trên, bạn sẽ tự tin giải quyết bài tập này một cách hiệu quả.