Bài 4.39 thuộc chương trình Toán 11 tập 1, sách Kết nối tri thức, là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này thường yêu cầu học sinh phải vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 4.39 trang 102, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB, SD; K là giao điểm của mặt phẳng (AMN) và đường thẳng SC. Tỉ số (frac{{SK}}{{SC}}) bằng: A. (frac{1}{2}) B. (frac{1}{3}) C. (frac{1}{4}) D. (frac{2}{3})
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB, SD; K là giao điểm của mặt phẳng (AMN) và đường thẳng SC. Tỉ số \(\frac{{SK}}{{SC}}\) bằng:
A. \(\frac{1}{2}\)
B. \(\frac{1}{3}\)
C. \(\frac{1}{4}\)
D. \(\frac{2}{3}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lý Menelaus để tính tỉ số.
Lời giải chi tiết
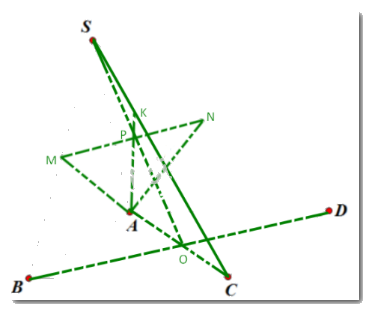
Gọi O là giao điểm AC và BD, gọi P là trung điểm MN
Ta có MN là đường trung bình tam giác SBD
Suy ra S, P, O thẳng hàng và P là trung điểm của SO
Do đó P thuộc SO hay P thuộc mp(SAC)
Trong mp(SAC), nối AP kéo dài cắt SC tại K
Suy ra K là giao điểm của SC và mp(AMN)
Áp dụng định lí Menelaus cho tam giác SOC:
\(\frac{{KS}}{{KC}} \times \frac{{CA}}{{AO}} \times \frac{{OP}}{{PS}} = 1\) suy ra \(\frac{{KS}}{{KC}} \times \frac{2}{1} \times 1 = 1\) suy ra \(\frac{{KS}}{{KC}} = \frac{1}{2}\)
Vậy \(\frac{{SK}}{{SC}} = \frac{1}{3}\)
Đáp án: B.
Bài 4.39 trang 102 SGK Toán 11 tập 1 - Kết nối tri thức là một bài toán quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Trước khi đi vào giải bài tập, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Bài 4.39 thường liên quan đến việc tìm đạo hàm của hàm số, khảo sát hàm số bằng đạo hàm, hoặc giải các bài toán tối ưu hóa.
Để giải Bài 4.39 trang 102 SGK Toán 11 tập 1 - Kết nối tri thức, chúng ta thực hiện theo các bước sau:
Giả sử bài toán yêu cầu tìm cực trị của hàm số f(x) = x3 - 3x2 + 2. Chúng ta sẽ thực hiện như sau:
Vậy hàm số f(x) có điểm cực đại là (0, 2) và điểm cực tiểu là (2, -2).
Khi giải Bài 4.39 trang 102 SGK Toán 11 tập 1 - Kết nối tri thức, các em cần lưu ý những điều sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Việc nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm là rất quan trọng đối với học sinh lớp 11, đặc biệt là những em có định hướng theo đuổi các ngành khoa học kỹ thuật.
Để củng cố kiến thức về Bài 4.39 trang 102 SGK Toán 11 tập 1 - Kết nối tri thức, các em có thể làm thêm các bài tập tương tự sau:
giaitoan.edu.vn hy vọng rằng lời giải chi tiết và hướng dẫn giải Bài 4.39 trang 102 SGK Toán 11 tập 1 - Kết nối tri thức sẽ giúp các em học sinh hiểu rõ hơn về bài tập này và tự tin giải các bài tập tương tự. Chúc các em học tốt!