Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Mục 5 trang 37 SGK Toán 11 tập 1 - Kết nối tri thức là một phần quan trọng trong chương trình học, đòi hỏi học sinh nắm vững kiến thức về hàm số và đồ thị.
Chúng tôi hiểu rằng việc tự giải bài tập có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, giúp bạn hiểu rõ bản chất của bài toán và áp dụng kiến thức vào các bài tập tương tự.
a) Quan sát Hình 1.25, hãy cho biết đường thẳng (y = - 1) cắt đồ thị hàm số (y = cot x) tại mấy điểm trên khoảng (left( {0;pi } right)?)
Video hướng dẫn giải
a) Quan sát Hình 1.25, hãy cho biết đường thẳng \(y = - 1\) cắt đồ thị hàm số \(y = \cot x\) tại mấy điểm trên khoảng \(\left( {0;\pi } \right)?\)
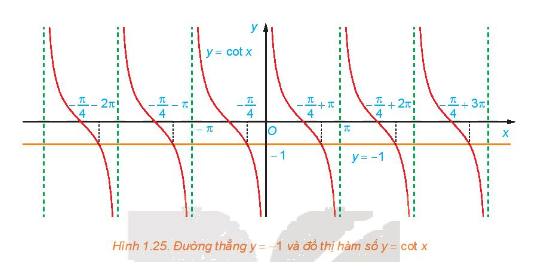b) Dựa vào tính tuần hoàn của hàm cotang, hãy viết công thức nghiệm của phương trình đã cho.
Phương pháp giải:
Nghiệm của phương trình \(\cot x = - 1\) là hoành độ các giao điểm của đường thẳng \(y = - 1\) và đồ thị hàm số \(y = \cot x\)
Lời giải chi tiết:
a) Từ Hình 1.25, ta thấy đường thẳng \(y = - 1\) cắt đồ thị hàm số \(y = \cot x\;\)tại 1 điểm \(x = - \frac{\pi }{4} + \pi \) trên khoảng \(\left( {0;\pi } \right)\)
b) Ta có công thức nghiệm của phương trình là: \(x = - \frac{\pi }{4} + \pi + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
Video hướng dẫn giải
Giải các phương trình sau:
a) \(\cot x = 1;\) b) \(\sqrt 3 \cot x + 1 = 0\)
Phương pháp giải:
Sử dụng công thức nghiệm \(\cot x = m\; \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \;\;\left( {k \in \mathbb{Z}} \right)\)
Lời giải chi tiết:
a) \(\cot x = 1\; \Leftrightarrow \cot x = \cot \frac{\pi }{4}\;\;\; \Leftrightarrow x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
b) \(\sqrt 3 \cot x + 1 = 0\;\;\; \Leftrightarrow \sqrt 3 \cot x = - 1\; \Leftrightarrow \cot x = - \frac{{\sqrt 3 }}{3}\;\; \Leftrightarrow \cot x = \cot \left( { - \frac{\pi }{3}} \right)\)
\( \Leftrightarrow x = - \frac{\pi }{3} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
Mục 5 trang 37 SGK Toán 11 tập 1 - Kết nối tri thức tập trung vào việc nghiên cứu về hàm số bậc hai và đồ thị của chúng. Đây là một chủ đề nền tảng trong chương trình Toán học, đóng vai trò quan trọng trong việc giải quyết các bài toán thực tế và xây dựng nền tảng cho các kiến thức nâng cao hơn.
Mục 5 bao gồm các nội dung chính sau:
Để giải các bài tập trong Mục 5 một cách hiệu quả, bạn cần nắm vững các kiến thức và kỹ năng sau:
Bài tập: Tìm tọa độ đỉnh và trục đối xứng của Parabol y = 2x2 - 8x + 6.
Giải:
Trong Mục 5, các bài tập thường gặp bao gồm:
Để học tốt Mục 5, bạn nên:
| Công thức | Mô tả |
|---|---|
| xđỉnh = -b/2a | Hoành độ đỉnh của Parabol |
| yđỉnh = f(xđỉnh) | Tung độ đỉnh của Parabol |
| Δ = b2 - 4ac | Biệt thức của phương trình bậc hai |
Hy vọng với những kiến thức và phương pháp giải được trình bày trên, bạn sẽ tự tin hơn khi giải các bài tập trong Mục 5 trang 37 SGK Toán 11 tập 1 - Kết nối tri thức. Chúc bạn học tập tốt!
