Bài 5.6 trang 109 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Kết nối tri thức, tập trung vào việc giải quyết các bài toán liên quan đến phép biến hình. Bài tập này giúp học sinh củng cố kiến thức về các phép biến hình và ứng dụng vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 5.6 trang 109, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
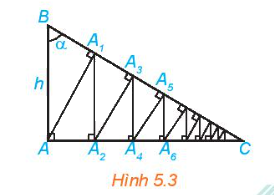
Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng (alpha ) (H.5.3). Từ A kẻ (A{A_1} bot BC), từ ({A_1}) kẻ ({A_1}{A_2} bot AC), sau đó lại kẻ ({A_2}{A_3} bot BC). Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn (A{A_1}{A_2}{A_3} ldots ) Tính độ dài đường gấp khúc này theo h và (alpha )
Đề bài
Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng \(\alpha \) (H.5.3). Từ A kẻ \(A{A_1} \bot BC\), từ \({A_1}\) kẻ \({A_1}{A_2} \bot AC\), sau đó lại kẻ \({A_2}{A_3} \bot BC\). Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn \(A{A_1}{A_2}{A_3} \ldots \) Tính độ dài đường gấp khúc này theo h và \(\alpha \)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào đề bài để tìm ra công thức tổng quát.
Lời giải chi tiết
Độ dài đường gấp khúc tạo thành cấp số nhân với số hạng tổng quát là:
\({u_n} = sin\;\alpha \; \times h \times {\left( {sin\;\alpha \;} \right)^{n - 1}}\).
Độ dài đường gập khúc: \(A{A_1} + {A_2}{A_3} + \ldots \).
Đây là tổng cấp số nhân lùi vô hạn với \({u_1} = sin\;\alpha \; \times h,\;q = sin\;\alpha \;\).
Nên \(A{A_1} + {A_2}{A_3} + \ldots = \frac{{sin\;\alpha \; \times h}}{{1 - sin\;\alpha \;}}\).
Bài 5.6 trang 109 SGK Toán 11 tập 1 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về phép biến hình, cụ thể là phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán hình học.
Bài tập 5.6 thường bao gồm các yêu cầu sau:
Để giải quyết bài tập này, học sinh cần nắm vững các kiến thức sau:
Dưới đây là ví dụ về cách giải một bài tập điển hình trong Bài 5.6:
Ví dụ: Cho điểm A(1; 2) và phép tịnh tiến theo vectơ v = (3; -1). Tìm ảnh A' của điểm A qua phép tịnh tiến đó.
Giải:
Áp dụng công thức phép tịnh tiến, ta có:
xA' = xA + vx = 1 + 3 = 4
yA' = yA + vy = 2 + (-1) = 1
Vậy, A'(4; 1).
Phép biến hình có nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức về Bài 5.6 trang 109 SGK Toán 11 tập 1 - Kết nối tri thức, các em học sinh có thể tự giải thêm các bài tập sau:
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về Bài 5.6 trang 109 SGK Toán 11 tập 1 - Kết nối tri thức và tự tin giải các bài tập tương tự. Chúc các em học tốt!