Chào mừng các em học sinh đến với bài giải chi tiết mục 4 trang 47, 48 sách giáo khoa Toán 11 tập 2 chương trình Kết nối tri thức. Bài viết này cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn là địa chỉ tin cậy dành cho các em học sinh muốn tìm kiếm sự hỗ trợ trong quá trình học tập môn Toán.
Một tài liệu hướng dẫn rằng đối với ghế bàn ăn, nên thiết kế lưng ghế tạo với mặt ghế một góc có số đo từ 100° đến 105°.
Video hướng dẫn giải
Một tài liệu hướng dẫn rằng đối với ghế bàn ăn, nên thiết kế lưng ghế tạo với mặt ghế một góc có số đo từ 100° đến 105°. Trong Hình 7.51, các tia Ox, Oy được vẽ tương ứng trên mặt ghế, lưng ghế đồng thời vuông góc với giao tuyến a của mặt ghế và lưng ghế.
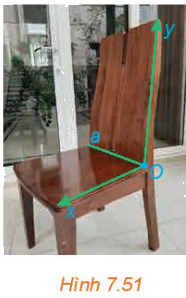
a) Theo tài liệu nói trên, góc nào trong hình nên có số đo từ 100° đến 105°?
b) Nếu thiết kế theo hướng dẫn đó thì góc giữa mặt phẳng chứa mặt ghế và mặt phẳng chứa lưng ghế có thể nhận số đo từ bao nhiêu đến bao nhiêu độ?
Phương pháp giải:
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng vuông góc vào giao tuyến hai mặt phẳng tại cùng một điểm.
Lời giải chi tiết:
a) Theo tài liệu nói trên, góc xOy trong hình nên có số đo từ 100° đến 105°
b) Vì các tia Ox, Oy được vẽ tương ứng trên mặt ghế, lưng ghế đồng thời vuông góc với giao tuyến a của mặt ghế và lưng ghế nên góc giữa lưng ghế và mặt ghế là góc giữa Ox và Oy mà góc xOy có số đo từ 100° đến 105°
Do đó nếu thiết kế theo hướng dẫn đó thì góc giữa mặt phẳng chứa mặt ghế và mặt phẳng chứa lưng ghế có thể nhận số đo 750 đến 800
Video hướng dẫn giải
Cho hình chóp S.ABC có SA \( \bot \) (ABC), AB = AC = a, \(\widehat {BAC} = {120^0},SA = \frac{a}{{2\sqrt 3 }}.\) Gọi M là trung điểm của BC.

a) Chứng minh rằng \(\widehat {SMA}\) là một góc phẳng của góc nhị diện [S, BC, A].
b) Tính số đo của góc nhị diện [S, BC, A].
Phương pháp giải:
Từ một điểm O bất kì thuộc cạnh a của góc nhị diện [P, a, Q], vẽ các tia Ox, Oy tương ứng thuộc (P), (Q) và vuông góc với a. Góc xOy được gọi là một góc phẳng của góc nhị diện [P, a, Q].
Lời giải chi tiết:
a) Xét tam giác ABC có AB = AC => tam giác ABC cân tại A mà M là trung điểm BC
=> \(AM \bot BC\) (1)
\(\begin{array}{l}SA \bot BC\left( {SA \bot \left( {ABCD} \right)} \right)\\ \Rightarrow BC \bot \left( {SAM} \right);SM \subset \left( {SAM} \right) \Rightarrow BC \bot SM\,\,\,\left( 2 \right)\end{array}\)
Từ (1), (2) ta có \(\widehat {SMA}\) là một góc phẳng của góc nhị diện [S, BC, A].
b) Xét tam giác ABC cân tại A có
\(\widehat {BAC} = {120^0} \Rightarrow \widehat {ACB} = {30^0}\)
\(\sin \widehat {ACB} = \frac{{AM}}{{AC}} \Leftrightarrow \sin {30^0} = \frac{{AM}}{a} \Leftrightarrow AM = \frac{a}{{2 }}\)
\(\tan \widehat {SMA} = \frac{{SA}}{{AM}} = \frac{a}{{2\sqrt 3 }}:\frac{a}{{2 }} = \frac{\sqrt 3}{3} \Rightarrow \widehat {SMA} = 30^0\)
Video hướng dẫn giải
Trong cửa sổ ở Hình 7.56, cánh và khung cửa là các nửa hình tròn có đường kính 80 cm, bản lề được đính ở điểm chính giữa O của các cung tròn khung và cánh cửa. Khi cửa mở, đường kính của khung và đường kính của cánh song song với nhau và cách nhau một khoảng d; khi cửa đóng, hai đường kính đó trùng nhau. Hãy tính số đo của góc nhị diện có hai nửa mặt phẳng tương ứng chứa cánh, khung cửa khi d = 40 cm.

Phương pháp giải:
Từ một điểm O bất kì thuộc cạnh a của góc nhị diện [P, a, Q], vẽ các tia Ox, Oy tương ứng thuộc (P), (Q) và vuông góc với a. Góc xOy được gọi là một góc phẳng của góc nhị diện [P, a, Q].
Lời giải chi tiết:
Gọi đường kính của khung là AB có tâm I và đường kính của cánh là MN có tâm I’
=> II’ = d = 40cm
Vì đường kính của khung và đường kính của cánh song song với nhau nên mặt phẳng chứa cánh song song với mặt phẳng chứa khung
=> Hai mặt phẳng đó cắt nhau tại 1 đường thẳng d’ qua O song song với AB và MN.
Vì O là điểm chính giữa nên \(OI \bot AB,OI' \bot MN\)
=> \(d' \bot OI,d' \bot OI'\)
Do đó góc nhị diện có hai nửa mặt phẳng tương ứng chứa cánh, khung cửa là góc \(\widehat {IOI'}\)
Xét tam giác IOI’ có
\(OI = OI' = \frac{{80}}{2} = 40 \Rightarrow OI = OI' = II'\)
\( \Rightarrow \) Tam giác IOI’ đều \( \Rightarrow \) \(\widehat {IOI'} = {60^0}\)
Vậy số đo của góc nhị diện có hai nửa mặt phẳng tương ứng chứa cánh, khung cửa khi d = 40 cm là 600
Mục 4 trang 47, 48 SGK Toán 11 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương 4: Hàm số lượng giác và ứng dụng của hàm số lượng giác. Nội dung chính bao gồm các dạng bài tập về xác định tính đơn điệu của hàm số lượng giác, tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác, và giải phương trình lượng giác cơ bản. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo và chuẩn bị cho kỳ thi sắp tới.
Để giải tốt các bài tập trong mục 4, học sinh cần nắm vững các phương pháp sau:
Đề bài: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2sin(x) + 1.
Lời giải:
Vì -1 ≤ sin(x) ≤ 1 với mọi x, ta có:
-2 ≤ 2sin(x) ≤ 2
-2 + 1 ≤ 2sin(x) + 1 ≤ 2 + 1
-1 ≤ y ≤ 3
Vậy, giá trị lớn nhất của hàm số là 3, đạt được khi sin(x) = 1, và giá trị nhỏ nhất của hàm số là -1, đạt được khi sin(x) = -1.
Để học tốt môn Toán 11, đặc biệt là phần Hàm số lượng giác, các em cần:
Hy vọng bài giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về mục 4 trang 47, 48 SGK Toán 11 tập 2 - Kết nối tri thức và đạt kết quả tốt trong học tập.