Bài 4.20 trang 87 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán liên quan đến quan hệ song song, vuông góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu Bài 4.20 trang 87 SGK Toán 11 tập 1, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
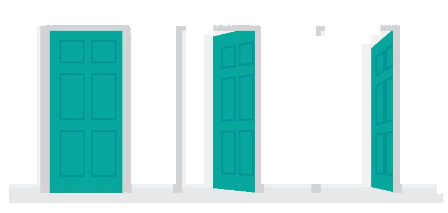
Bạn Nam quan sát thấy dù cửa ra vào được mở ở vị trí nào thì mép trên của cửa luôn song song với một mặt phẳng cố định. Hãy cho biết đó là mặt phẳng nào và giải thích tại sao.
Đề bài
Bạn Nam quan sát thấy dù cửa ra vào được mở ở vị trí nào thì mép trên của cửa luôn song song với một mặt phẳng cố định. Hãy cho biết đó là mặt phẳng nào và giải thích tại sao.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b song song với a.
Lời giải chi tiết
Ta có: Mép trên của cửa luôn song song với mép dưới của cửa.
Và khi cửa được mở ra , dù được mở ở vị trí nào thì mép dưới của cửa cũng thuộc mặt sàn. Vì vậy mép trên của cửa luôn song song với mặt phẳng sàn cố định.
Bài 4.20 trang 87 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về quan hệ song song và vuông góc trong không gian. Để giải bài tập này, học sinh cần nắm vững các định lý và tính chất liên quan đến đường thẳng và mặt phẳng.
Đề bài yêu cầu chúng ta chứng minh một số quan hệ hình học giữa các đường thẳng và mặt phẳng. Việc phân tích kỹ đề bài, xác định các yếu tố đã cho và yêu cầu chứng minh là bước đầu tiên quan trọng để giải quyết bài toán.
a) Chứng minh SC ⊥ (ABCD)
Để chứng minh SC ⊥ (ABCD), ta cần chứng minh SC vuông góc với hai đường thẳng bất kỳ nằm trong mặt phẳng (ABCD). Ta có:
Từ đó, ta có thể suy ra SC ⊥ (ABCD).
b) Chứng minh BD ⊥ (SCD)
Để chứng minh BD ⊥ (SCD), ta cần chứng minh BD vuông góc với hai đường thẳng bất kỳ nằm trong mặt phẳng (SCD). Ta có:
Từ đó, ta có thể suy ra BD ⊥ (SCD).
c) Tính góc giữa hai đường thẳng SB và (ABCD)
Gọi H là hình chiếu vuông góc của S lên AC. Do SA ⊥ (ABCD) nên H trùng với A. Góc giữa SB và (ABCD) chính là góc SBA.
Ta có: tan(SBA) = SA/AB = SA/a. Do đó, góc SBA = arctan(SA/a).
Khi giải các bài tập về quan hệ song song và vuông góc trong không gian, học sinh cần chú ý:
Để rèn luyện thêm kỹ năng giải toán, học sinh có thể tham khảo các bài tập tương tự trong SGK Toán 11 tập 1 - Kết nối tri thức và các tài liệu tham khảo khác.
Bài 4.20 trang 87 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng, giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán về quan hệ song song và vuông góc trong không gian. Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ giải quyết bài tập này một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!