Bài 3.5 trang 67 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Kết nối tri thức. Bài học này tập trung vào việc giải quyết các bài toán liên quan đến đạo hàm của hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Hãy cùng khám phá lời giải chi tiết của Bài 3.5 trang 67 SGK Toán 11 tập 1 ngay dưới đây!
Tuổi thọ (năm) của 50 bình ắc quy ô tô được cho như sau: Tuổi thọ (năm) (left[ {2;2,5} right)) (left[ {2,5;3} right)) (left[ {3;3,5} right)) (left[ {3,5;4} right)) (left[ {4;4,5} right)) (left[ {4,5;5} right)) Tần số (4) (9) (14) (11) (7) (5) a) Xác định mốt và giải thích ý nghĩa b) Tính tuổi thọ trung bình của 50 bình ắc quy ô tô này
Đề bài
Tuổi thọ (năm) của 50 bình ắc quy ô tô được cho như sau:

a) Xác định mốt và giải thích ý nghĩa.
b) Tính tuổi thọ trung bình của 50 bình ắc quy ô tô này.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:
Bước 1: Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm \(j:\left[ {{a_j};\;{a_{j + 1}}} \right)\).
Bước 2: Mốt được xác định là: \({M_0} = {a_j} + \frac{{{m_j} - {m_{j - 1}}}}{{\left( {{m_j} - {m_{j - 1}}} \right) + \left( {{m_j} - {m_{j + 1}}} \right)}}.h\).
Trong đó \({m_j}\) là tần số của nhóm j (quy ước \({m_0} = {m_{k + 1}} = 0)\) và h là độ dài của nhóm
Sử dụng công thức số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\bar x\)\(\bar x = \frac{{{m_1}{x_1} + \ldots + {m_k}{x_k}}}{n}\).
Trong đó \(n = {m_1} + \ldots + {m_k}\) là cỡ mẫu và là giá trị đại diện của nhóm \(\left[ {{a_i},{a_{i + 1}}} \right)\).
Lời giải chi tiết
14 là tần số lớn nhất nên mốt thuộc nhóm \(\left[ {3;3,5} \right),\) ta có:
\(j = 3,{a_3} = 3,{m_3} = 14,{m_2} = 9,{m_4} = 11,h = 0,5\).
Do đó \({M_0} = 3 + \frac{{14 - 9}}{{\left( {14 - 9} \right) + \left( {14 - 11} \right)}} \times 0,5 = 3,31\).
b)
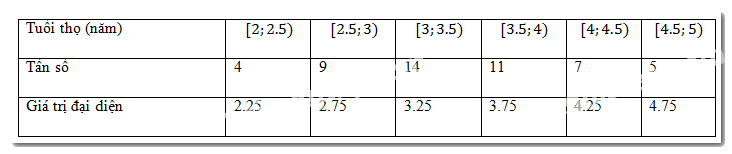
Tuổi thọ trung bình:
\(\bar x = \frac{{4 \times 2,25 + 9 \times 2,75 + 14 \times 3,25 + 11 \times 3,75 + 7 \times 4,25 + 5 \times 4,75}}{{50}} = 3,48\).
Bài 3.5 trang 67 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học về đạo hàm. Để giải bài tập này, học sinh cần nắm vững các kiến thức về định nghĩa đạo hàm, các quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.
Bài tập 3.5 yêu cầu học sinh tính đạo hàm của các hàm số sau:
Áp dụng quy tắc tính đạo hàm của tổng và hiệu, ta có:
y' = 3x2 - 6x + 2
Áp dụng quy tắc tích, ta có:
y' = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
Áp dụng quy tắc chia, ta có:
y' = [(1)(x - 1) - (x + 1)(1)] / (x - 1)2 = (x - 1 - x - 1) / (x - 1)2 = -2 / (x - 1)2
Áp dụng quy tắc hàm hợp, ta có:
y' = cos(2x) * 2 = 2cos(2x)
Đạo hàm có rất nhiều ứng dụng trong toán học và các lĩnh vực khác, bao gồm:
Để củng cố kiến thức về đạo hàm, bạn có thể luyện tập thêm các bài tập sau:
Bài 3.5 trang 67 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về đạo hàm và các ứng dụng của nó. Hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh có thể tự tin giải bài tập và nắm vững kiến thức về đạo hàm.