Bài 1.3 trang 16 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Kết nối tri thức, tập trung vào việc giải quyết các bài toán liên quan đến vectơ. Bài học này giúp học sinh củng cố kiến thức về vectơ, phép toán vectơ và ứng dụng của vectơ trong hình học.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong Bài 1.3, giúp học sinh nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau:
Đề bài
Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau:
a) \(\frac{{2\pi }}{3}\); b) \( - \frac{{11\pi }}{4}\); c) \({150^0}\); d) \( - {225^0}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Để biểu diễn các góc lượng giác trên đường tròn lượng giác ta thường sử dụng các kết quả sau
- Góc \(\alpha \) và góc \(\alpha + k2\pi ,k\; \in \;\mathbb{Z}\) có cùng điểm biểu diễn trên đường tròn lượng giác.
- Số điểm trên đường tròn lượng giác biểu diễn bởi số đo có dạng \(\alpha + \frac{{k2\pi }}{m}\) (với k là số nguyên và m là số nguyên dương). Từ đó để biểu diễn các góc lượng giác đó ta lần lượt cho k từ 0 tới (m – 1) rồi biểu diễn các góc đó.
Lời giải chi tiết
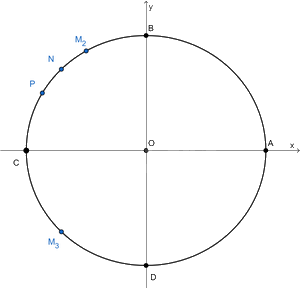
a) Ta có: \(\frac{{\frac{{2\pi }}{3}}}{{2\pi }} = \frac{1}{3}\). Ta chia đường tròn thành 3 phần bằng nhau. Khi đó điểm \({M_2}\) là điểm biểu diễn bởi góc có số đo \(\frac{{2\pi }}{3}\).
b) Ta có \( - \frac{{11\pi }}{4} = - \frac{{3\pi }}{4} + \left( { - 1} \right).2\pi \). Do đó điểm biểu diễn bởi góc \( - \frac{{11\pi }}{4}\) trùng với góc \( - \frac{{3\pi }}{4}\) và là điểm \({M_3}\).
c) Ta có \(\frac{{150}}{{180}} = \frac{5}{6}\). Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó P là điểm biểu diễn bởi góc \({150^0}\)
d) Ta có \( - {225^0} = - {180^0} - {45^0}\). Do đó điểm biểu diễn N là điểm biểu diễn bởi góc \( - {225^0}\)
Bài 1.3 trang 16 SGK Toán 11 tập 1 - Kết nối tri thức là một phần quan trọng trong chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán thực tế. Dưới đây là giải chi tiết từng bài tập trong bài, cùng với hướng dẫn và các lưu ý quan trọng.
Đề bài: Cho hai vectơ a và b. Tính a + b và a - b.
Giải: Để tính tổng và hiệu của hai vectơ, ta thực hiện phép cộng hoặc trừ các thành phần tương ứng của chúng. Ví dụ, nếu a = (x1, y1) và b = (x2, y2) thì:
(Giải thích chi tiết hơn với các ví dụ cụ thể về các giá trị của x1, y1, x2, y2)
Đề bài: Cho vectơ a = (2, -3) và số thực k = 3. Tính ka.
Giải: Để nhân một vectơ với một số thực, ta nhân mỗi thành phần của vectơ với số thực đó. Ví dụ:
ka = (kx1, ky1)
Trong trường hợp này, ka = 3(2, -3) = (6, -9).
(Giải thích chi tiết hơn về ý nghĩa của phép nhân vectơ với một số thực)
Đề bài: Tính tích vô hướng của hai vectơ a = (1, 2) và b = (-3, 4).
Giải: Tích vô hướng của hai vectơ a = (x1, y1) và b = (x2, y2) được tính theo công thức:
a ⋅ b = x1x2 + y1y2
Trong trường hợp này, a ⋅ b = (1)(-3) + (2)(4) = -3 + 8 = 5.
(Giải thích ý nghĩa của tích vô hướng và ứng dụng của nó trong việc xác định góc giữa hai vectơ)
Hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh có thể tự tin giải quyết Bài 1.3 trang 16 SGK Toán 11 tập 1 - Kết nối tri thức. Chúc các bạn học tốt!