Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 105, 106 sách giáo khoa Toán 11 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt nhất trong môn Toán.
Cho dãy số (left( {{u_n}} right)) với ({u_n} = frac{{{{left( { - 1} right)}^n}}}{n}) a) Biểu diễn năm số hạng đầu của dãy số này trên trục số b) Bắt đầu từ số hạng nào của dãy, khoảng cách từ ({u_n}) đến 0 nhỏ hơn 0,01?
Video hướng dẫn giải
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{n}\)
a) Biểu diễn năm số hạng đầu của dãy số này trên trục số.
b) Bắt đầu từ số hạng nào của dãy, khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,01?
Phương pháp giải:
Dựa vào công thức số hạng tổng quát tìm được 5 số hạng đầu tiên và biểu diễn trên trục số.
Lời giải chi tiết:
a) \({u_1} = - 1;\;\;{u_2} = \frac{1}{2};\;\;\;{u_3} = - \frac{1}{3};\;\;\;{u_4} = \frac{1}{4};\;\;\;{u_5} = - \frac{1}{5}\).
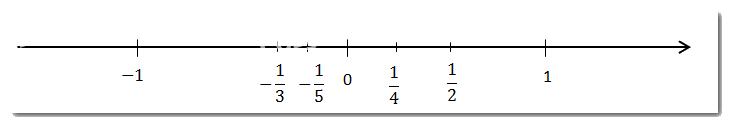
b) Ta có: \({u_{100}} = 0,01\) suy ra bắt đầu từ số hạng thứ 101 khoảng cách từ số hạng đến 0 nhỏ hơn 0,01.
Video hướng dẫn giải
Chứng minh rằng: \(\mathop {lim}\limits_{n \to + \infty } \frac{{{{\left( { - 1} \right)}^{n - 1}}}}{{{3^n}}}\; = 0\).
Phương pháp giải:
Ta nói dãy số \(\left( {{u_n}} \right)\) có giới hạn là 0 khi n dần tới dương vô cực, nếu \(\left| {{u_n}} \right|\) có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi.
Lời giải chi tiết:
\(\left| {{u_n}} \right| = \frac{{{{\left( { - 1} \right)}^{n - 1}}}}{{{3^n}}}\) có thể nhỏ hơn một số dương bé tùy ý khi n đủ lớn.
Ta có: \(\left| {{u_n}} \right| < 1.69 \times {10^{ - 5}}\) ta cần n > 10.
Vậy các số hạng của dãy số kể từ số hạng thứ 11 đều có giá trị nhỏ hơn \(1.69 \times {10^{ - 5}}\).
Video hướng dẫn giải
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{n + {{\left( { - 1} \right)}^n}}}{n}\). Xét dãy số \(\left( {{v_n}} \right)\) xác định bởi \({v_n} = {u_n} - 1\). Tính \(\mathop {lim}\limits_{n \to + \infty }{v_n}\;\).
Phương pháp giải:
Dãy sô \(\left( {{u_n}} \right)\) có giới hạn là số thực a khi n dần tới dương vô cực nếu \(\left( {{u_n} - a} \right)\; = 0\).
Lời giải chi tiết:
\({u_n} = {u_n} - 1 = \frac{{n + {{\left( { - 1} \right)}^n}}}{n} - 1 = \frac{{n + {{\left( { - 1} \right)}^n} - n}}{n} = \frac{{{{\left( { - 1} \right)}^n}}}{n} \to 0\) khi \(n \to + \infty \).
Do vậy \({v_n}\; = 0\).
Video hướng dẫn giải
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{{{3.2}^n} - 1}}{{{2^n}}}\). Chứng minh rằng \(\mathop {lim}\limits_{n \to + \infty } {u_n} = 3\).
Phương pháp giải:
\({u_n}\; = a\) khi và chỉ khi \(\left( {{u_n} - a} \right)\; = 0\).
Lời giải chi tiết:
\({u_n} = \frac{{3 \times {2^n} - 1}}{{{2^n}}} - 3 = \frac{{3 \times {2^n} - 1 - 3 \times {2^n}}}{{{2^n}}} = - \frac{1}{{{2^n}}} \to 0\) khi \(n \to + \infty \).
Do vậy \({u_n}\; = 3\).
Video hướng dẫn giải
Một quả bóng cao su được thả từ độ cao 5 m xuống một mặt sàn. Sau mỗi lần chạm sàn, quả bóng nảy lên độ cao bằng \(\frac{2}{3}\) độ cao trước đó. Giả sử rằng quả bóng luôn chuyển động vuông góc với mặt sàn và quá trình này tiếp diễn vô hạn lần. Giả sử \({u_n}\) là độ cao (tính bằng mét) của quả bóng sau lần nảy lên thứ n. Chứng minh rằng dãy số \(\left( {{u_n}} \right)\) có giới hạn là 0.
Phương pháp giải:
\({u_n}\; = a\) khi và chỉ khi \(\left( {{u_n} - a} \right)\; = 0\).
Tìm được độ cao của quả bóng sau mỗi lần chạm sàn là cấp số nhân.
Lời giải chi tiết:
Độ cao quả bóng sau 1 lần chạm sàn: \({u_1} = 5.\frac{2}{3}\) (m).
Độ cao quả bóng sau 2 lần chạm sàn: \({u_2} = 5.{\left( {\frac{2}{3}} \right)^2}\) (m).
…
Độ cao quả bóng sau n lần chạm sàn: \({u_n} = 5.{\left( {\frac{2}{3}} \right)^n}\) (m).
Vì \(|q| = \frac{2}{3} < 0\) nên \({u_n} = 5.{\left( {\frac{2}{3}} \right)^n}\) là một cấp số nhân lùi vô hạn.
Khi đó giới hạn của \({u_n} = 5.{\left( {\frac{2}{3}} \right)^n}\) bằng 0.
Mục 1 trang 105, 106 SGK Toán 11 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số và đồ thị hàm số bậc hai. Đây là một phần quan trọng trong chương trình Toán 11, là nền tảng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo. Việc nắm vững các khái niệm, định lý và kỹ năng giải bài tập trong mục này là rất cần thiết để đạt kết quả tốt trong môn Toán.
Để xác định các hệ số a, b, c của hàm số bậc hai y = ax2 + bx + c, ta cần đưa hàm số về dạng tổng quát. Sau đó, đối chiếu với dạng tổng quát để xác định các hệ số tương ứng.
Ví dụ: Cho hàm số y = 2x2 - 3x + 1. Xác định các hệ số a, b, c.
Giải: Hàm số đã ở dạng tổng quát y = ax2 + bx + c. Vậy a = 2, b = -3, c = 1.
Để vẽ đồ thị hàm số bậc hai, ta thực hiện các bước sau:
Ví dụ: Vẽ đồ thị hàm số y = x2 - 4x + 3.
Giải:
Vẽ parabol qua các điểm (2, -1), (0, 3), (1, 0) và (3, 0).
Để giải phương trình bậc hai ax2 + bx + c = 0, ta sử dụng công thức nghiệm:
x1,2 = (-b ± √(b2 - 4ac)) / 2a
Ví dụ: Giải phương trình x2 - 5x + 6 = 0.
Giải:
a = 1, b = -5, c = 6
Δ = (-5)2 - 4*1*6 = 1
x1 = (5 + √1) / 2 = 3
x2 = (5 - √1) / 2 = 2
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 105, 106 SGK Toán 11 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!