Bài 7.3 trang 30 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Kết nối tri thức. Bài học này tập trung vào việc giải quyết các bài toán liên quan đến đạo hàm của hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Cho tứ diện ABCD có (widehat {CBD} = {90^0}.)
Đề bài
Cho tứ diện ABCD có \(\widehat {CBD} = {90^0}.\)
a) Gọi M, N tương ứng là trung điểm của AB, AD. Chứng minh rằng MN vuông góc BC.
b) Gọi G, K tương ứng là trọng tâm của các tam giác ABC, ACD. Chứng minh rằng GK vuông góc với BC.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song song với b.
Lời giải chi tiết
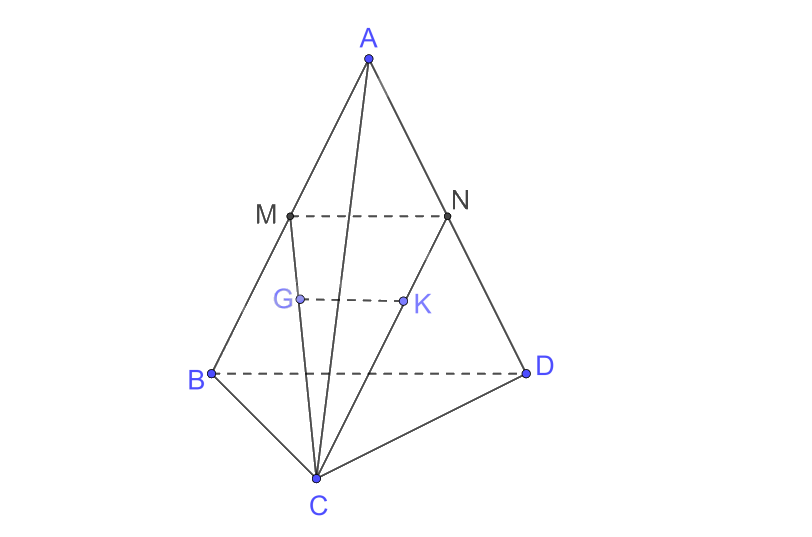
a) Xét tam giác ABD có
M, N tương ứng là trung điểm của AB, AD
\( \Rightarrow \) MN là đường trung bình của tam giác ABD
\( \Rightarrow \) MN // BD mà BD \( \bot \) BC (\(\widehat {CBD} = {90^0}\))
\( \Rightarrow \) MN \( \bot \) BC.
b) Vì G, K tương ứng là trọng tâm của các tam giác ABC, ACD nên \(\frac{{CG}}{{CM}} = \frac{{CK}}{{CN}} = \frac{2}{3}\)
\( \Rightarrow \) GK // MN (Định lý Talet) mà MN \( \bot \) BC
\( \Rightarrow \) GK \( \bot \) BC.
Bài 7.3 trang 30 SGK Toán 11 tập 2 – Kết nối tri thức là một phần quan trọng trong chương trình học về đạo hàm của hàm số. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm định nghĩa, các quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
Bài tập 7.3 bao gồm các câu hỏi và bài tập khác nhau, yêu cầu học sinh:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập 7.3, chúng tôi cung cấp hướng dẫn giải chi tiết cho từng câu hỏi và bài tập. Hướng dẫn này bao gồm:
Ví dụ 1: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = 3x2 + 4x - 5
Ví dụ 2: Tìm đạo hàm của hàm số g(x) = sin(x) tại x = π/2.
Giải:
g'(x) = cos(x)
g'(π/2) = cos(π/2) = 0
Khi giải bài tập 7.3, học sinh cần lưu ý:
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Để học tập và ôn luyện kiến thức về đạo hàm, học sinh có thể tham khảo các tài liệu sau:
Bài 7.3 trang 30 SGK Toán 11 tập 2 – Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách nắm vững các quy tắc tính đạo hàm và luyện tập thường xuyên, học sinh có thể giải quyết các bài tập một cách hiệu quả và ứng dụng đạo hàm vào giải quyết các bài toán thực tế.