Chào mừng bạn đến với bài học về Lý thuyết Đạo hàm cấp hai trong chương trình Toán 11 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và quan trọng nhất về đạo hàm cấp hai, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, ý nghĩa, cách tính đạo hàm cấp hai, và các ứng dụng thực tế của nó trong việc phân tích hàm số và giải quyết các bài toán tối ưu hóa.
1. Khái niệm đạo hàm cấp hai
1. Khái niệm đạo hàm cấp hai
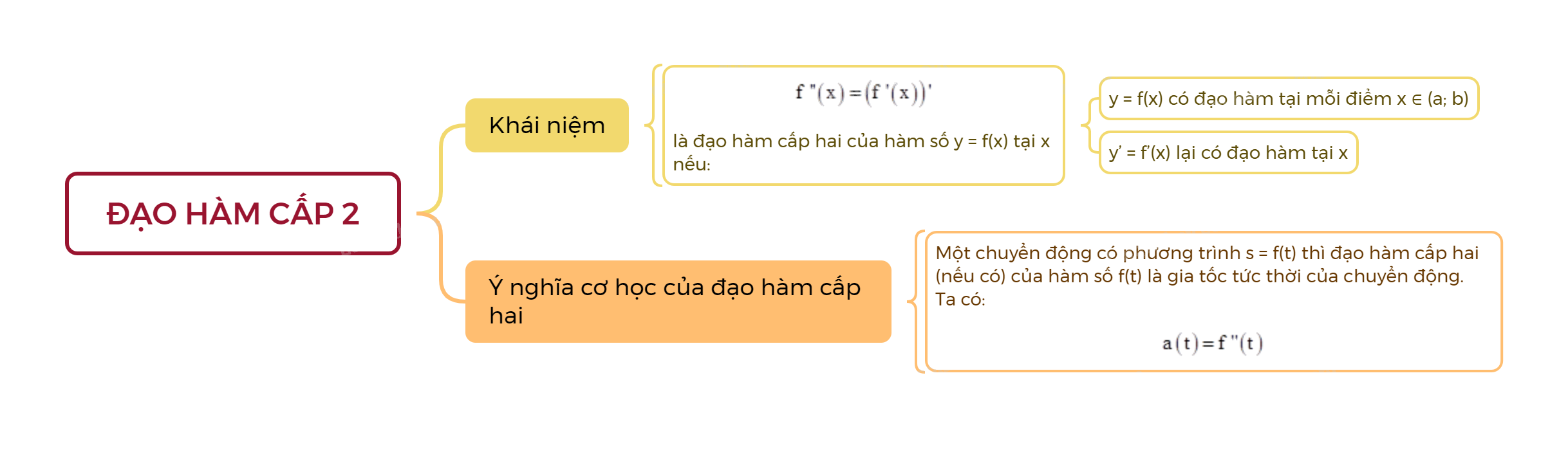
Giả sử hàm số y = f(x) có đạo hàm tại mỗi điểm \(x \in \left( {a;b} \right)\). Nếu hàm số y’ = f’(x) lại có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số y = f(x) tại x, kí hiệu là y” hoặc f”(x).
\(f''\left( x \right) = \left( {f'\left( x \right)} \right)'\).
2. Ý nghĩa cơ học của đạo hàm cấp hai
Một chuyển động có phương trình s = f(t) thì đạo hàm cấp hai (nếu có) của hàm số f(t) là gia tốc tức thời của chuyển động. Ta có:
\(a\left( t \right) = f''\left( t \right)\).
Đạo hàm cấp hai, hay đạo hàm bậc hai, là đạo hàm của đạo hàm bậc nhất của một hàm số. Nó cung cấp thông tin quan trọng về độ cong của đồ thị hàm số và giúp xác định các điểm cực trị, điểm uốn. Việc nắm vững lý thuyết đạo hàm cấp hai là nền tảng để giải quyết nhiều bài toán trong chương trình Toán 11 và các chương trình nâng cao hơn.
Cho hàm số y = f(x) có đạo hàm f'(x). Nếu f'(x) có đạo hàm, đạo hàm đó được gọi là đạo hàm cấp hai của f(x), ký hiệu là f''(x) hoặc y''.
Công thức tính đạo hàm cấp hai:
f''(x) = (f'(x))'
Đạo hàm cấp hai cho biết tốc độ thay đổi của đạo hàm bậc nhất. Nó liên quan mật thiết đến tính lồi và lõm của đồ thị hàm số:
Để tính đạo hàm cấp hai, ta thực hiện các bước sau:
Ví dụ:
Cho hàm số y = x3 - 3x2 + 2x + 1
Bước 1: Tính đạo hàm bậc nhất:
y' = 3x2 - 6x + 2
Bước 2: Tính đạo hàm cấp hai:
y'' = 6x - 6
Đạo hàm cấp hai có nhiều ứng dụng quan trọng trong việc phân tích hàm số:
Bài 1: Tính đạo hàm cấp hai của hàm số y = sin(2x)
Giải:
y' = 2cos(2x)
y'' = -4sin(2x)
Bài 2: Tìm điểm uốn của hàm số y = x4 - 4x3 + 6x2 - 4x + 1
Giải:
y' = 4x3 - 12x2 + 12x - 4
y'' = 12x2 - 24x + 12 = 12(x-1)2
y'' = 0 khi x = 1. Vì y'' luôn không âm, x = 1 không phải là điểm uốn.
Lý thuyết Đạo hàm cấp hai là một phần quan trọng của chương trình Toán 11 Kết nối tri thức. Việc hiểu rõ định nghĩa, ý nghĩa, cách tính và ứng dụng của đạo hàm cấp hai sẽ giúp bạn giải quyết các bài toán liên quan một cách hiệu quả và chính xác. Hãy luyện tập thường xuyên để nắm vững kiến thức này nhé!